Projection Methods for incompressible Navier Stokes Equations
One of the difficulty for the numerical simulation of incompressible Navier Stokes system is that the velocity and the pressure are coupled by the incompressibility constraint. In 1960s, by Chorin and Temam, the projection methods provide decoupling to overcome this difficulty. The most attractive feature of projection methods is that one only needs to solve a sequence of decoupled elliptic equations for the velocity and the pressure for each time steps.Related Works
[3] S. Lee, A.J. Salgado; Stability analysis of pressure correction schemes for the Navier-Stokes equations with traction boundary conditions; Computer Methods in Applied Mechanics and Engineering 2016 doi: 10.1016/j.cma.2016.05.043 [arXiv] [Journal][2] A. Bonito, J-L. Guermond, S. Lee; Modified Pressure-Correction Projection Methods: Open Boundary and Variable Time Stepping; Numerical Mathematics and Advanced Applications - ENUMATH 2013, Lecture Notes in Computational Science and Engineering, 103, 623--631, 2015. [preprint] [Link]
[1] S. Lee Numerical Simulations of the Bouncing Jets, PhD Thesis, Texas A&M University, 2014. [preprint] [TAMU]
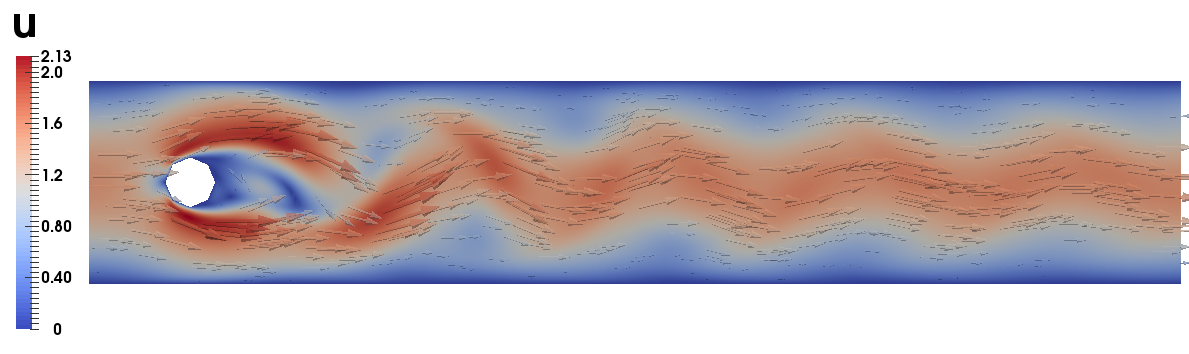
Using rotational pressure correction with traction boundary conditions

References
[1] J.-L. Guermond, P. Minev, J. Shen, An Overview of Projection methods for incompressible flows,
Computer Methods in Applied Mechanics and Engineering, 195 (2006) 6011--6045.
[2] J.-L. Guermond, P. Minev, J. Shen, Error analysis of pressure-correction schemes for the Navier-Stokes equations with open boundary conditions,
SIAM J. Numer. Anal., 43 1 (2005) 239--258.
