Enriched Galerkin Approximations
Related Works
[in Preparation] S. Lee, Y-J. Lee, M.F. Wheeler; Enriched Galerkin approximation for coupled flow and transport in porous media[12] T. Kadeethum, H.M. Nick, S. Lee, F. Ballarin Enriched Galerkin Discretization for Modelling Poroelasticity and Permeability Alteration in Heterogeneous Porous Media, 2021, DOI:https://doi.org/10.1016/j.jcp.2020.110030, Journal of Computational Physics,
[11] A. Rupp, S.Lee; Continuous Galerkin and enriched Galerkin methods with arbitrary order discontinuous trial functions for the elliptic and parabolic problems with jump conditions, Journal of Scientific Computing, 84, 9, 2020
[10] W. Choi, S. Lee; Optimal Error Estimate of Elliptic Problems with Dirac Sources, 2019, Applied Numerical Mathematics, https://doi.org/10.1016/j.apnum.2019.09.010
[9] T. Kadeethum, H.M. Nick, S. Lee, F. Ballarin Enriched Galerkin Discretization for Modelling Poroelasticity and Permeability Alteration in Heterogeneous Porous Media, submitted, 2019
[8] T. Kadeethum, H. M. Nick, and S. Lee Comparison of Two- and Three-field Formulation Discretizations for Flow and Solid Deformation in Heterogeneous Porous Media International Association for Mathematical Geosciences, 2019
[7] T. Kadeethum, H.M. Nick, S. Lee, C.N. Richardson, S. Salimzadeh, F. Ballarin A Novel Enriched Galerkin Method for Modelling Coupled Flow and Mechanical Deformation in Heterogeneous Porous Media American Rock Mechanics Association,2019
[6] Rencheng Dong, M.F. Wheeler, S. Lee; Numerical Simulation of Matrix Acidizing in Fractured Carbonate Reservoirs Using Adaptive Enriched Galerkin Method 2019, SPE-193862-MS, SPE RSC 2019, https://doi.org/10.2118/193862-MS
[5] J.Choo, S. Lee; Enriched Galerkin Finite Element Method for Locally Mass Conservative Simulation of Coupled Hydromechanical Problems 2018, Proceedings of China-Europe Conference on Geotehcnical Engineering, Springer Nature Switzerland AG
[4] J. Choo, S.Lee; Enriched Galerkin finite elements for coupled poromechanics with local mass conservation, 2018 November, Volume 341, Pages 311-332 Computer Methods in Applied Mechanics and Engineering, [Journal]
[3] S. Lee, M.F. Wheeler; Enriched Galerkin approximation for two phase flow in porous media with capillary pressure, Journal of Computational Physics, Volume 367, 15 August 2018, Pages 65-86, https://doi.org/10.1016/j.jcp.2018.03.031 [Preprint] [Journal]
[2] S. Lee, M.F. Wheeler; Adaptive enriched Galerkin methods for miscible displacement problems with entropy residual stabilization, Journal of Computational Physics, Volume 331, 15 February 2017, Pages 19-37, DOI: 10.1016/j.jcp.2016.10.072 [Journal]
[1] S. Lee, Y-J. Lee, M.F. Wheeler; A Locally Conservative Enriched Galerkin Approximation and Efficient Solver for the Parabolic Problems; DOI: 10.1137/15M1041109, SIAM SISC 2016 [Journal]
The advantages for using EG
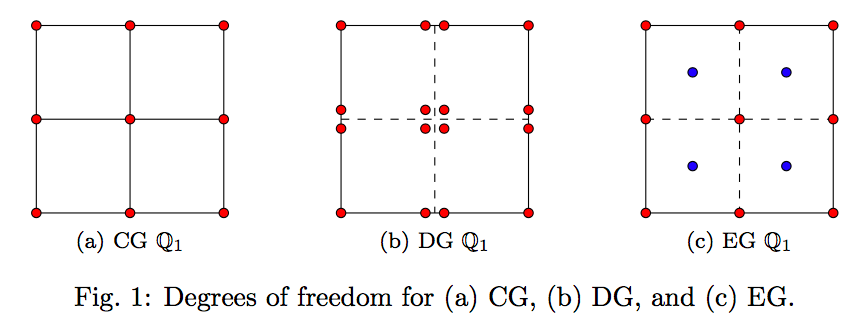
- Locally conservative flux.
- Less degrees of freedom compare to that of DG.
- Hihger order discretization is available.
- Efficient Solver is provided.
Related Other References
[1] S. Sun and J. Liu, A locally conservative finite element method based on enrichment of the continuous Galerkin method, SIAM Journal on Scientific Computing, 31(4), 2528-2548, 2009.[2] R. Becker, E. Burman, P. Hansbo, and M. G. Larson, A Reduced P1-Discontinuous Galerkin Method, Chalmers Finite Element Center Preprint 2003-13, Chalmers University of Technology, Goteborg, Sweden, 2003


