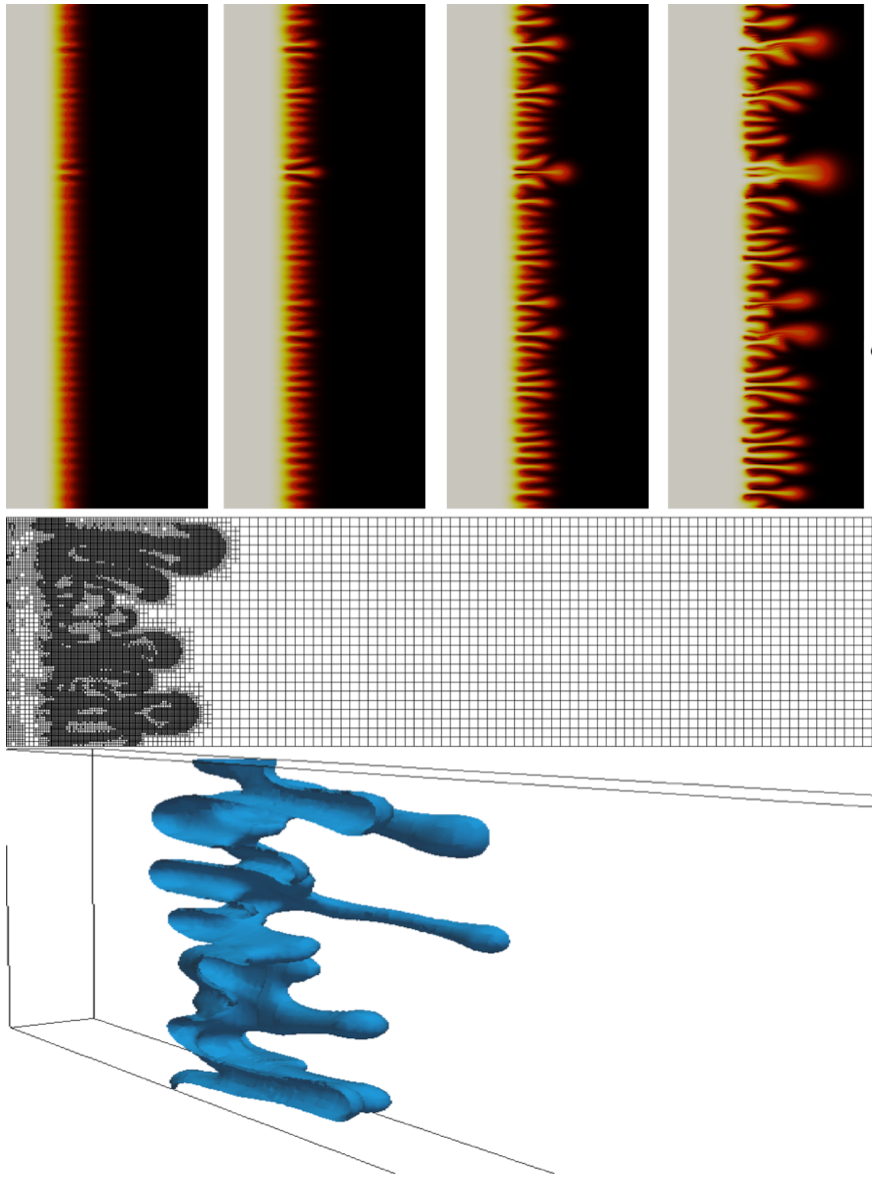
Viscous Fingering: Miscible Displacement
Related Works
[In preparation] S. Lee, Y-J. Lee, M.F. Wheeler; Enriched Galerkin approximations coupled flow and transport in porous media.[4] S. Lee, M.F. Wheeler; Enriched Galerkin approximation for two phase flow in porous media with capillary pressure, Journal of Computational Physics, Volume 367, 15 August 2018, Pages 65-86, https://doi.org/10.1016/j.jcp.2018.03.031 [Preprint] [Journal]
[3] G. Scovazzi, M.F. Wheeler, A. Mikeli\'c, S. Lee Analytical and variational numerical methods for unstable miscible displacement flows in porous media. Journal of Computational Physics , Volume 335, 15 April 2017, Pages 444-496, DOI: 10.1016/j.jcp.2017.01.021 [Preprint] [Journal]
[2] S. Lee, M.F. Wheeler; Adaptive enriched Galerkin methods for miscible displacement problems with entropy residual stabilization, Journal of Computational Physics , Volume 331, 15 February 2017, Pages 19-37, DOI: 10.1016/j.jcp.2016.10.072 [Journal]
[1] S. Lee, Y-J. Lee, M.F. Wheeler; A Locally Conservative Enriched Galerkin Approximation and Efficient Solver for the Parabolic Problems; DOI: 10.1137/15M1041109, SIAM SISC 2016 [Journal]
Viscous Fingering in Hele Shaw with Adaptive Mesh Refinement
Miscible displacement of one fluid by another in a porous medium has attracted considerable attention in subsurface modeling with emphasis on enhanced oil recovery applications. Recently, viscous fingering has been applied for proppant-filled hydraulic fracture propagation to efficiently transport the proppant to the tip of fractures. We present a novel approach to the simulation of miscible displacement by employing an adaptive enriched Galerkin finite element methods (EG) coupled with entropy residual stabilization for transport. EG is formulated by enriching the conforming continuous Galerkin finite element method (CG) with piecewise constant functions. EG provides locally and globally conservative fluxes, which is crucial for coupled flow and transport problems. Moreover, EG has fewer degrees of freedom in comparison with discontinuous Galerkin (DG) and an efficient flow solver has been derived which allows for higher order schemes. Finally, we note that it is crucial to have dynamic mesh adaptivity in order to reduce computational costs for large-scale three dimensional applications; both for flow and transport. For theoretical and computational details regarding EG for flow and transport the reader is referred to the following papers [Lee-Lee-Wheeler 2015] [Lee-Wheeler 2016].