Sanghyun Lee, PhD
Integrated Phase field Advanced Crack Simulator (IPACS) Ver3.0 Manual DownloadM.F. Wheeler*, T. Wick, S. Lee; IPACS: Integrated Phase-Field Advanced Crack Propagation Simulator. An adaptive, parallel, physics-based-discretization phase-field framework for fracture propagation in porous media, Computer Methods in Applied Mechanics and Engineering, Volume 367, 1 August 2020, 113124, https://doi.org/10.1016/j.cma.2020.113124 [Journal]
Related Works
[10] S. Lee, M. F. Wheeler; Modeling interactions of natural and two phase fluid filled fracture propagation in porous media, Computational Geoscience, DOI: 10.1007/s10596-020-09975-0, 2020, [Journal][9] M.F. Wheeler, S. Srinivasan, S. Lee, M. Singh; Unconventional Reservoir Management Modeling Coupling Diffusive Zone/Phase Field Fracture Modeling and Fracture Probability Maps, 2019, SPE 193830-MS, SPE RSC 2019, https://doi.org/10.2118/193830-MS [SPE]
[8] S. Shiozawa, S. Lee, M.F. Wheeler; The effect of stress boundary conditions on fluid-driven fracture propagation in porous media using a phase field modeling approach 2019, International Journal for Numerical and Analytical Methods in Geomechanics, DOI: 10.1002/nag.2899 [Journal]
[7] B. Min, S. Lee, M. F. Wheeler; Optimal hydraulic fracturing design using the phase field model coupled with global-objective genetic algorithm, Computational Geosciences, 2018, doi:10.1007/s10596-018-9728-6 [Preprint] [Journal]
[6] S. Lee, M.F. Wheeler, T. Wick; Iterative coupling of flow, geomechanics and adaptive phase-field fracture including a level-set crack width approach, Journal of Computational and Applied Mathematics, Volume 314, April 2017, Pages 40-60, DOI: 10.1016/j.cam.2016.10.022 [arXiv] [Journal]
[5] S. Lee, J.E. Reber , N.W. Hayman, M. F. Wheeler; Investigation of wing crack formation with a combined phase-field and experimental approach Geophysical Research Letters 43, 7946-7952, DOI: 10.1002/2016GL069979, 2016 [Preprint] [Journal]
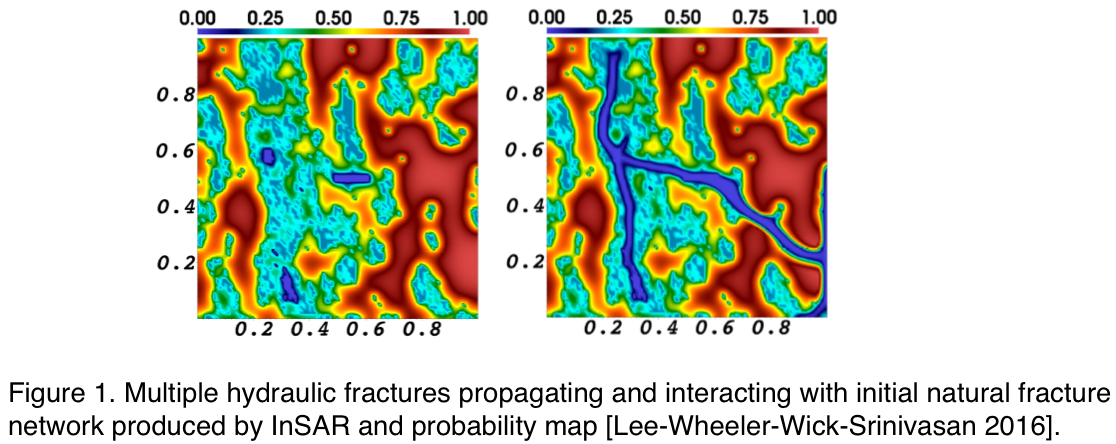
[4] S. Lee, M.F. Wheeler, T. Wick, S. Srinivasan; Initialization of phase-field fracture propagation in porous media using probability maps of fracture networks; Mechanics Research Communications, DOI: 10.1016/j.mechrescom.2016.04.002, 2016 [Journal]
[3] S. Lee, M. Mikelic, M. F. Wheeler, T. Wick; Phase-field modeling of proppant-filled fractures in a poroelastic medium, Comp. Meth. Appl. Mech. Engrg., doi : 10.1016/j.cma.2016.02.008, 2016; [Journal]
[2] S. Lee, M.F. Wheeler, T. Wick; Pressure and fluid-driven fracture propagation in porous media using an adaptive finite element phase field model Comp. Meth. Appl. Mech. Engrg., doi : 10.1016/j.cma.2016.02.037, 2016; [Journal]
[1] T. Wick, S. Lee, M.F. Wheeler; 3D Phase-field for pressurized fracture propagation in heterogeneous media; VI International Conference on Computational Methods for Coupled Problems in Science and Engineering 2015 Proceedings; [preprint] [e-book]
Current Research : Fracture Propagation in Porous Media using Phase Field
The design and evaluation of hydraulic fracturing jobs are critical for efficient production from shale oil and gas fields. The efficiency depends on the interaction between hydraulic and naturally occurring discrete fractures. A rigorous fracture propagation model is there fore necessary to predict fracture growth pattern in a heterogeneous, anisotropic poroelastic medium.We study the lower-dimensional fracture surface approximated by a phase field function, where phase field is an indicator function with diffusive crack zones, which is based on gamma-convergent approximations of free discontinuity problems. The most important advantages for using the phase field is that fracture nucleation, propagation, kinking, and curvilinear paths are automatically induced in the model; post-processing of street intensity factors and re-meshing resolving the crack path are avoided.
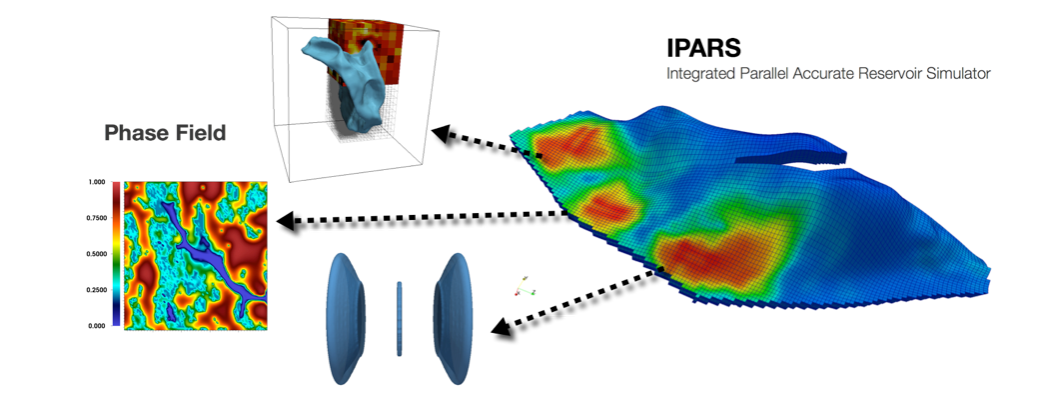
0. Overview
1. History
i) Motivation- Production benefits: Shale gas, tight gas.
- Environmental and health issues.
- Coupled problem: Flow and geomechanics.
- Classical theory of crack propagation
- Griffith 1921, Irwin 1958, and Barenblatt 1962.
- Crack
with length
advances if energy release rate is critical :
whereis the potential energy and
the fracture toughness.
- Variational methods based on energy minimization
-
-convergent approximations of free discontinuity problems. Mumford-Shah 1985, Ambrosio-Tortorelli 1992, Giacomini 2003
- Geomechanics Modeling: Introduce diffusive crack zones. Francfort-Marigo 1998, Francfort-Larson 2003, Bourdin 2007
-
- Other FEM based numerical implementations.
- Sharp crack discontinuities.
- Interface element, Element and nodal enrichment strategies.
- XFEM, GFEM, Belytschko 2003,2009, Miehe 2007, Gupta 2014
- Bunger-Detournay-Garagash-Peirce 2007
2. Phase Field
- Phase field interpolates between the unbroken and the broken states. Miehe-Welschinger-Hofacker 2010
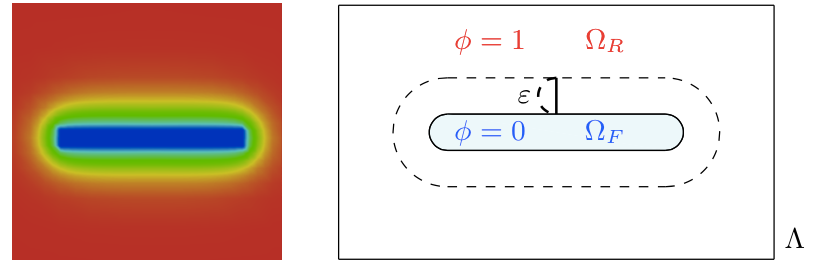
- Crack nucleation, propagation, and the path are automatically determined.
- Joining and branching of (multiple) cracks are simple to handle.
- Fixed-topology approach : re-meshing is avoided.
- As an indicator function, theory and numerical simulations show promising findings for future ideas.
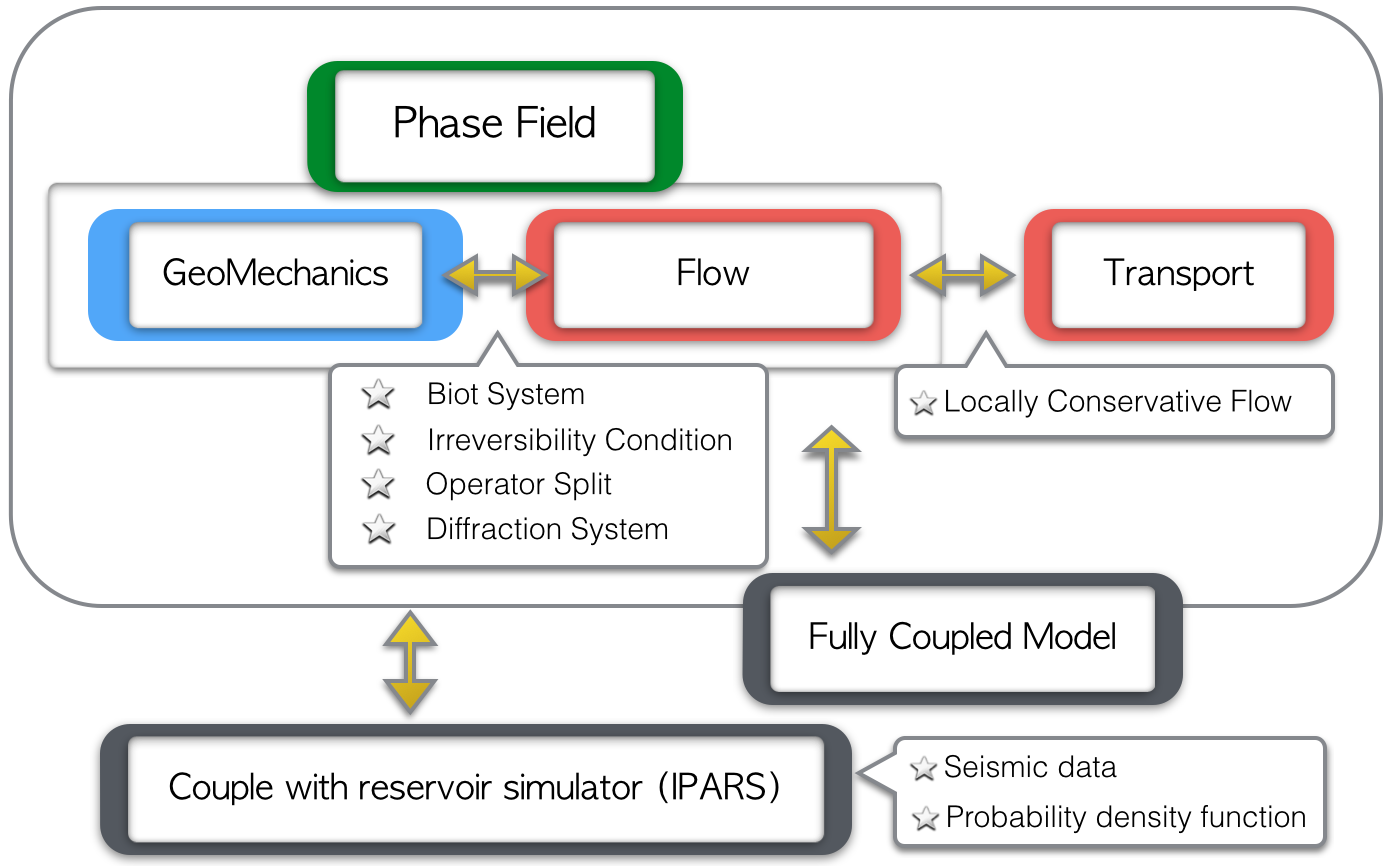
3. Modeling and Numerical Methods
i) Geomechaincs- Energy Minimization with irreversibility constraint.
- Solve monolithically or decouple the displacement and the phase field. [Mikelic-Wick-Wheeler]
- Simple penalization [Mikelic-Wick-Wheeler]
- Augmented Lagrangian[Wick-Wheeler-Wollner 2013]
- Active set [Heister-Wick-Wheeler 2015]
- Biot System : Couple with pressure from porous media.
- Pressure diffraction system. [Mikelic-Wick-Wheeler 2015]
- Fixed stress split to couple geomechnacis and flow. [Mikelic-Wheeler]
- Extend to 3D computations [L.-Wick-Wheeler 2015]
- Locally Conservative Flow
- Projection Method. [Sun-Wheeler 2006]
- Enriched Galerkin Method. [Sun-Liu 2009] [L.Lee-Wheeler]
- Discontinuous Galerkin- piecewise constant
- Predictor-Corrector Method [Heister-Wick-Wheeler 2015]
5. Numerical Results: Validation
- Elasticity : Miehe Shear Test
- Constant Pressure
- Sneddon Test [Sneddon 1969] [Miehe et al 2012] [Gupta-Duarte 2014]
- Stress Shadowed Effect

6. Numerical Examples
Multiple Fractures Joining and Branching in Heterogeneous Media 3D |
|---|



|
Parallel Multiple Fractures Growing; Shadowed Stress Effect |
|---|




|
- Joining and Branching fractures in 3D Heterogeneous Media
- 3D Fluid Filled Penny Shaped Fracture


