National Science Fonudation (NSF) Divison of Mathematical Sciecne (DMS) Project

Research Outcome Report
DMS-#2208402: Collaborative Research: Physics-Preserving Adaptive Finite Element Methods for Thermo-Poroelasticity
06/01/2022 - 5/31/2024   $240,220.00

Abstract :  Geothermal energy is one of the most promising renewable energy sources and has proven to be reliable, clean, and safe. When designing enhanced geothermal systems (EGS), it is necessary to understand the multiscale, multiphysics, thermal-hydraulic-mechanical (THM) processes that impact the EGS dynamics and productivity. This project aims to gain a fundamental understanding of key mechanisms controlling the dynamics in EGS (solid displacement, fluid flow, and heat transfer) and sustainability of EGS reservoirs through numerical simulations. A novel numerical simulation framework to be built through this project will allow for designing, managing, and optimizing energy production from EGS. The THM processes in EGS can be described by Biot?s thermo-poroelasticity model, a coupled system of nonlinear partial differential equations. Any desirable numerical methods for THM systems should preserve the underlying physical laws, such as mass and energy conservation, and present no numerical instabilities for a wide range of physical and simulation parameters. This project seeks to develop a unified numerical modeling framework based on adaptive enriched Galerkin (EG) methods to provide robust and physics-preserving numerical methods whose numerical analysis is feasible. The proposed EG schemes are mass conservative and free of numerical instabilities commonly present in poroelasticity and coupled flow-transport problems. The mass conservation property, stability, and convergence behaviors of the proposed methods will be studied mathematically and confirmed numerically. Moreover, residual-based a posteriori error estimators will be derived and utilized for designing dynamic mesh adaptivity techniques. The developed EG algorithms will be implemented within finite element software packages to verify the theoretical results and validate the new numerical model's capabilities to capture the EGS dynamics. The performance of the new EG methods will be compared with that of state-of-the-art numerical methods. NSF Webpage Click Here

The following journal papers are the outcome of the project for each objectives

Objective 1: Development of Enriched Galerkin methods for THM systems

[1] S. Lee, S-Y Yi Locking-free and locally-conservative enriched Galerkin method for poroelasticity, Journal of Scientific Computing volume 94, Article number: 26 (2023)
❀ Link to the journal
❀ Abstract: This paper develops a new coupled enriched Galerkin (EG) scheme for Biot’s poroelasticity model based on the displacement-pressure formulation. The aim of this work is to provide a stable and robust numerical method for a wide range of physical and numerical parameters. The finite-dimensional solution spaces are enriched linear Lagrange spaces, and the inf-sup condition between the two spaces is achieved by adding a stabilization term. The resulting coupled EG method is locally conservative and provides stable solutions without spurious oscillations or overshoots/undershoots. The well-posedness and optimal a priori error estimates are established. Numerical results in various scenarios are provided.
➪ Highlights :

[2] S-Y Yi, S. Lee Physics-preserving enriched Galerkin method for a fully-coupled thermo-poroelasticity model, submitted
❀ Link to the jouranl
❀ Abstract This paper proposes a new numerical method for a fully-coupled, quasi-static thermo-poroelasticity model in a unified enriched Galerkin (EG) method framework. In our method, the mechanics sub-problem is solved using a locking-free EG method, and the flow and heat sub-problems are solved using a locally-conservative EG method. The proposed method offers mass and energy conservation properties with much lower costs than other methods with the same properties, including discontinuous Galerkin methods and mixed finite element methods. The well-posedness and optimal a priori error estimates are carefully derived. Several numerical tests confirm the theoretical optimal convergence rates and the mass and energy conservation properties of the new method.
➪ Highlights

Objective 2: Development of iterative methods for THM systems

[3] F. Ballarin, S. Lee, S-Y. Yi Convergence of iterative coupling scheme for thermo-poroelasticity, submitted
❀ Link to the journal
❀ Abstract : This paper considers an iterative coupling scheme for solving thermo-poroelasticity problems. The methods we develop extend the idea of the fixed-stress splitting scheme extensively studied for Biot's poroelasticity and are based on the continuous Galerkin method. We carefully examine convergence criteria in terms of various parameters, such as material properties. We also determine the optimal stabilization parameters that lead to the fastest convergence. Numerical experiments are performed to validate the convergence analysis and demonstrate the effectiveness of our fixed-stress iteration scheme. The results provide insights into the convergence behavior of our iterative coupling scheme beyond theory and highlight the importance of selecting proper stabilization parameters.
➪ Highlights

Objective 3: with a Ph.D student : Enriched Galerkin methods for THM systems and a posteriori error estimators

[4] S. Lee, Y. Yang Comparisons of finite element methods for coupled Darcy's flow and transport problems; local mass conservation and maximum principle, submitted
❀ Link to the journal
❀ Abstract: This paper explores a variety of finite element method pairs for the numerical solution of coupled flow and transport problems in porous media. The study focuses on the challenges posed by heterogeneous domains in two and three dimensions, where preserving important physical properties, such as the maximum principle for transport and local mass conservation for flow, is crucial. Failure to uphold these properties can lead to errors like spurious oscillations and deviations from accurate solution values. The finite element methods investigated in this study encompass continuous Galerkin (CG), discontinuous Galerkin (DG), enriched Galerkin (EG), and mixed methods (Raviart-Thomas). The research underscores the significance of locally conservative fluxes, which are provided by DG, EG, and mixed methods, in mitigating spurious oscillations in coupled flow and transport problems. The study also examines the performance of the discrete maximum principle achieved through the lowest order of the DG scheme or the CG formulation with a first-order artificial viscosity stabilizer for transport. Numerical tests are presented to evaluate the strengths and weaknesses of different finite element method pairs for flow and transport simulations.
➪ Highlights



Preliminary Research Outcomes for the Pending Proposal

1. Modeling Hydrauilc-Mechanical-Chemcial System in Proous Media
2. Machine Learning coupled with Finite Element Methods

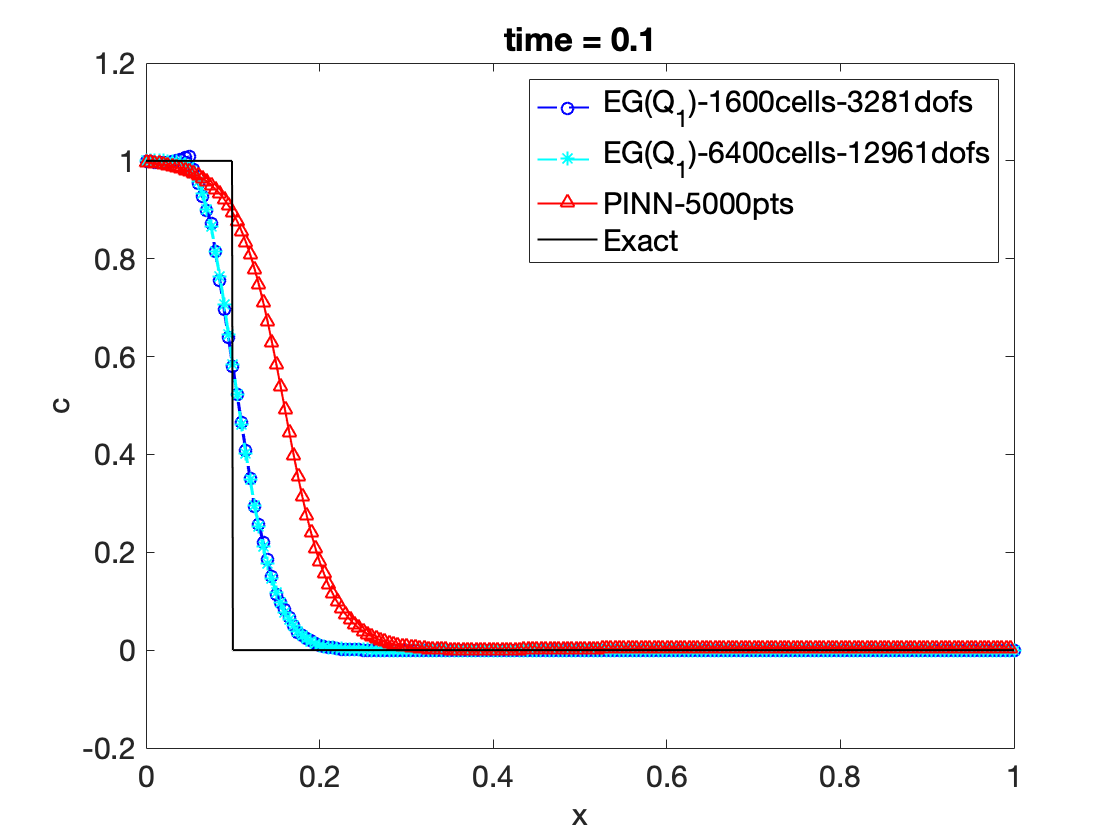
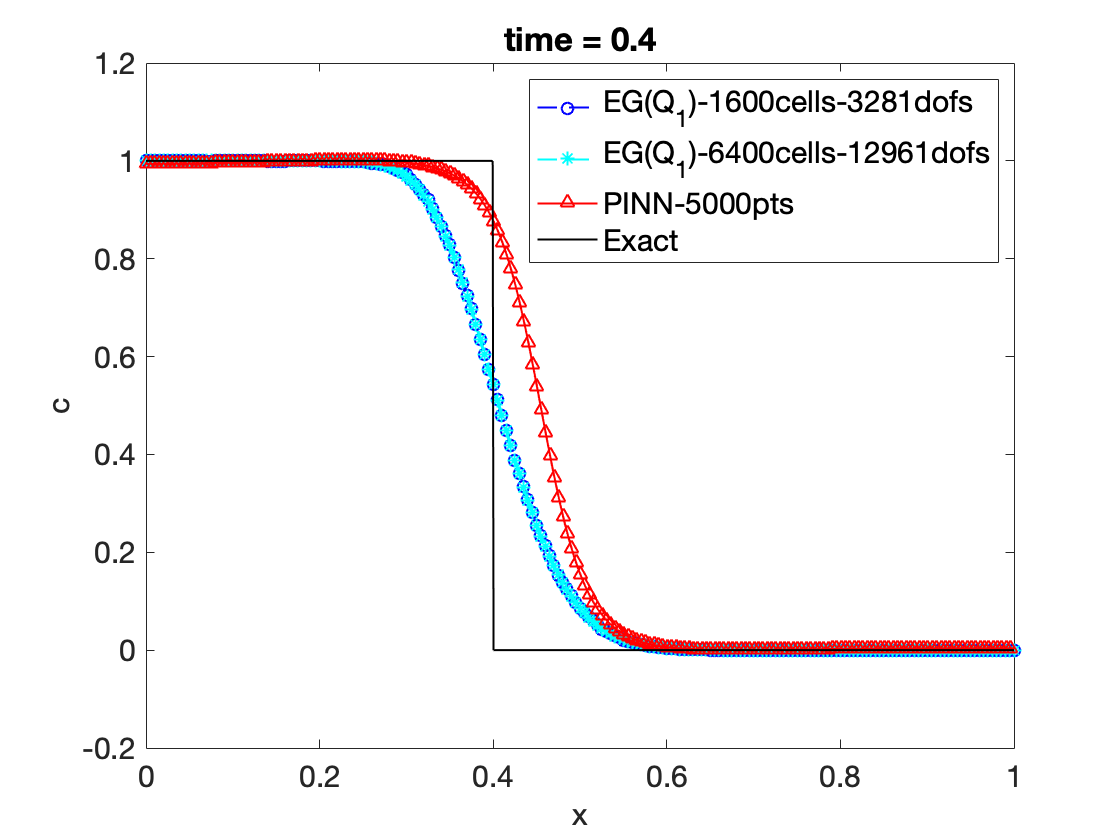
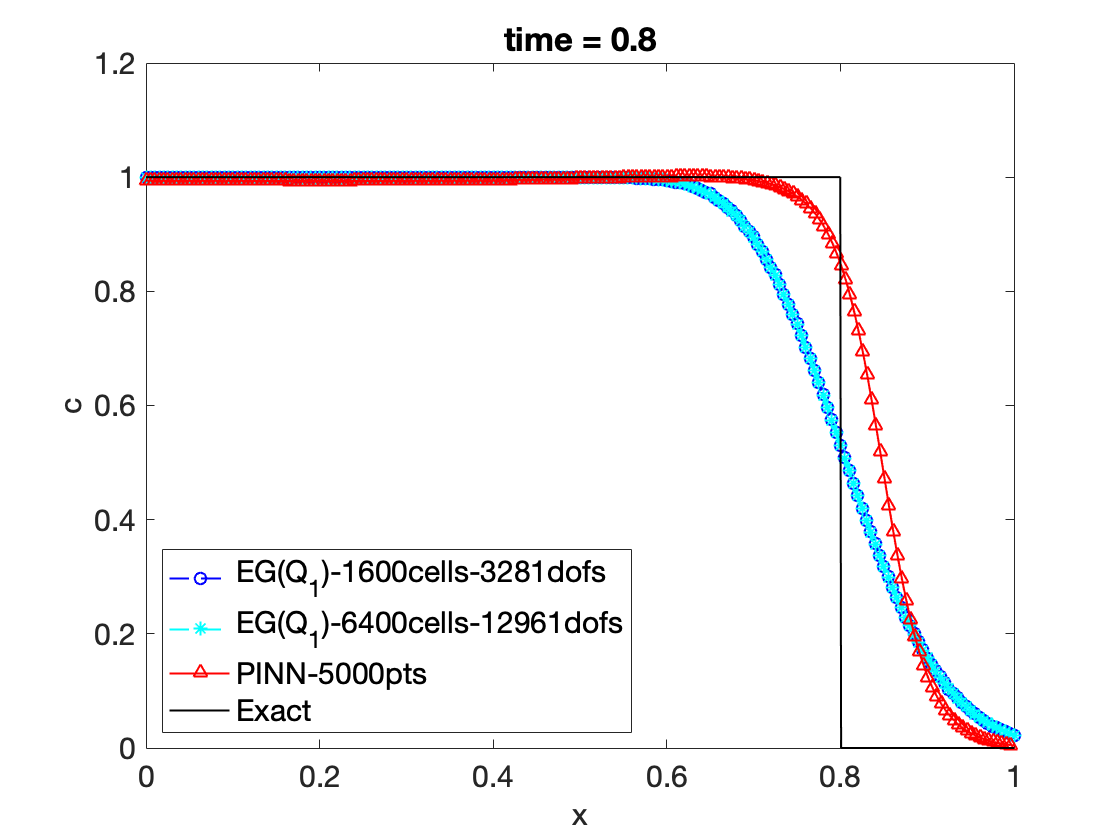
3. Scientific Machine Learning :: Physics Informed Neural Network



Research Outcome Report
DMS-#1913016:: Fluid-filled Fracture Propagation with a Phase Field Approach in Subsurface
                  by Employing Nonlinear Strain Limiting Models and Enriched Galerkin Methods
                  08/01/2019 - 7/31/2021   $99,116.00

Abstract : The project aims to investigate the way in which pressurized and fluid-filled cracks or fractures spread through subsurface materials. In porous materials such as soils and rocks, the flow of the fluids through the material's pores can force significant deformations (such as cracks and fractures) to occur in the solid porous media. These poromechanical interactions are crucial to many important problems such as tunnel construction, subsidence, dam or levee failure, and CO2 sequestration.
The classic mathematical model governing the spread of these deformations is formulated by coupling linear elasticity or poroelasticity with deformation systems. However, one of the major disadvantages of classical linear elasticity models is that strain values are linearly proportional to stress values. Thus, it contradicts the assumptions of the model, and it may not accurately predict realistic scenarios. This project focuses on establishing the nonlinear strain limiting model, a new class of theoretical model. The advantage of the nonlinear strain limiting models over classical linearized models is that strain remains bounded even if the stress tends to infinity, which is critical for fluid-filled fractures. The new model will be extended to consider poroelasticity. Next, the poroelasticity model will be coupled with a phase field approach to implement quasi-static fluid-filled fracture propagation. Moreover, the novel enriched Galerkin (EG) finite element approximations will be employed in the project to address several crucial issues for numerical discretization. It is well known that classical Galerkin finite element methods generally do not guarantee local mass conservation, which could lead to non-physical oscillation. EG methods will be investigated to overcome these challenges, and their stability and convergence for the poroelasticity system will be analyzed. The findings will then be used to develop a forecasting tool to predict the path of quasi-static fracture propagation and will be utilized to evaluate and validate the performance of these new models. NSF Webpage Click Here

The following journal papers are the outcome of the project for each objectives

Objective 1: Development of Enriched Galerkin methods for related problems

[1] W. Choi, S. Lee, Optimal Error Estimate of Elliptic Problems with Dirac Sources, 2019, Applied Numerical Mathematics, Volume 150, April 2020, Pages 76-104.
❀ Link to the journal
❀ Abstract: We present an optimal a priori error estimates of the elliptic problems with Dirac sources away from the singular point using discontinuous and enriched Galerkin finite element methods. It is widely shown that the finite element solutions for elliptic problems with Dirac source terms converge sub-optimally in classical norms on uniform meshes. However, here we employ inductive estimates and norm to obtain the optimal order by excluding the small ball regions with the singularities for both two and three dimensional domains. Numerical examples are presented to substantiate our theoretical results.
➪ Highlights :
  • Provide studies in the optimal convergence rate for discontinuos and enriched Galerkin methods with singularities
  • This finding allows to utilize the FEM to thin fractures and injection/production sources
  • The following figure illustrates the optimal convergence rate for multiple Dirac sources; when it is far from the singularities


[2] T. Kadeethum, H.M. Nick, S. Lee, F. Ballarin Enriched Galerkin Discretization for Mixed-Dimensional Modelling Flow in Fractured Porous Media, Advances in Water Resources, Volume 142, August 2020, 103620.
❀ Link to the journal
❀ Abstrct: This paper presents the enriched Galerkin discretization for modeling fluid flow in fractured porous media using the mixed-dimensional approach. The proposed method has been tested against published benchmarks. Since fracture and porous media discontinuities can significantly influence single- and multi-phase fluid flow, the heterogeneous and anisotropic matrix permeability setting is utilized to assess the enriched Galerkin performance in handling the discontinuity within the matrix domain and between the matrix and fracture domains. Our results illustrate that the enriched Galerkin method has the same advantages as the discontinuous Galerkin method; for example, it conserves local and global fluid mass, captures the pressure discontinuity, and provides the optimal error convergence rate. However, the enriched Galerkin method requires much fewer degrees of freedom than the discontinuous Galerkin method in its classical form. The pressure solutions produced by both methods are similar regardless of the conductive or non-conductive fractures or heterogeneity in matrix permeability. This analysis shows that the enriched Galerkin scheme reduces the computational costs while offering the same accuracy as the discontinuous Galerkin so that it can be applied for large-scale flow problems. Furthermore, the results of a time-dependent problem for a three-dimensional geometry reveal the value of correctly capturing the discontinuities as barriers or highly-conductive fractures.
➪ Highlights :
  • A novel mixed-dimensional enriched Galerkin presented for fluid flow in fractured porous media
  • Enriched Galerkin provides accurate solutions capturing discontinuities with coarse meshes
  • Positive aspects of the enriched Galerkin with mixed-dimensional paradigm are highlighted
  • The following figures illustrate the flow and pressure in three dimensoinal domain (based on the real field data) with fractures



[3] Rupp, A., Lee, S. Continuous Galerkin and Enriched Galerkin Methods with Arbitrary Order Discontinuous Trial Functions for the Elliptic and Parabolic Problems with Jump Conditions. J Sci Comput 84, 9 (2020)
❀ Link to the journal
❀ Abstract: In this paper, a new version of the enriched Galerkin (EG) method for elliptic and parabolic equations is presented and analyzed, which is capable of dealing with a jump condition along a submanifold \Gamma_LG. The jump condition is known as Henry's law in a stationary diffusion process. Here, the novel EG finite element method is constructed by enriching the continuous Galerkin finite element space by not only piecewise constants but also with piecewise polynomials with an arbitrary order. In addition, we extend the proposed method to consider new versions of a continuous Galerkin (CG) and a discontinuous Galerkin (DG) finite element method. The presented uniform analyses for CG, DG, and EG account for a spatially and temporally varying diffusion tensor which is also allowed to have a jump at \Gamma_LG and gives optimal convergence results. Several numerical experiments verify the presented analyses and illustrate the capability of the proposed methods.
➪ Highlights :
  • A new approach for continous and enriched Galerkin finite element methods for handling discontinuites are established
  • Optimal error convergence for elliptic and time dependent parabolic equations are presented
  • The following figure illustrates the solution values for each time step (n), where three circles in the domain contains discontinuity in the coefficients


[4] T. Kadeethum, H.M. Nick, S. Lee, F. Ballarin, Enriched Galerkin Discretization for Modelling Poroelasticity and Permeability Alteration in Heterogeneous Porous Media, Volume 427, 15 February 2021, 110030, Journal of Computational Physics, 2021
❀ Link to the journal
❀ Abstract: In this paper, we utilize the enriched Galerkin (EG) finite element method for the flow equation in Biot's system, which provides a robust locally conservative flux in heterogeneous porous media. The computational algorithm to solve the coupled system with the permeability alteration is presented with the linearization and Picard's iterative scheme. The block structure is utilized for the linear system in numerical discretization, and the computer code is shared in the open-source platform. In the numerical experiments, we compare the proposed EG method with the classical continuous Galerkin (CG) and discontinuous Galerkin (DG) finite element methods in different scenarios, including the North sea reservoirs setup. While DG and EG methods provide similar approximations for the pressure solutions, the CG method produces spurious oscillations in fluid pressure and volumetric strain solutions near the material interfaces, especially for the soft materials. The difference of flux approximation between EG and DG methods is insignificant; still, the EG method demands approximately two and three times fewer degrees of freedom than the DG method for two- and three-dimensional geometries. ➪ Highlights :
  • Enriched Galerkin for coupled solid deformation and flow in heterogeneous media.
  • A new block structure proposed to compose the enriched Galerkin function space.
  • Linearization and iterative schemes utilized for media permeability alteration.
  • Positive and negative aspects of the enriched Galerkin highlighted.


[5] T. Kadeethum, S. Lee, H.M. Nick, Finite Element Solvers for Biot's Poroelasticity Equations in Porous Media, Math Geosci 52, 977-1015, 2020
❀ Link to the journal
❀ Abstract: We study and compare five different combinations of finite element spaces for approximating the coupled flow and solid deformation system, so-called Biot's equations. The permeability and porosity fields are heterogeneous and depend on solid displacement and fluid pressure. We provide detailed comparisons among the continuous Galerkin, discontinuous Galerkin, enriched Galerkin, and two types of mixed finite element methods. Several advantages and disadvantages for each of the above techniques are investigated by comparing local mass conservation properties, the accuracy of the flux approximation, number of degrees of freedom (DOF), and wall and CPU times. Three-field formulation methods with fluid velocity as an additional primary variable generally require a larger number of DOF, longer wall and CPU times, and a greater number of iterations in the linear solver in order to converge. The two-field formulation, a combination of continuous and enriched Galerkin function space, requires the fewest DOF among the methods that conserve local mass. Moreover, our results illustrate that three out of the five methods conserve local mass and produce similar flux approximations when conductivity alteration is included. These comparisons of the key performance indicators of different combinations of finite element methods can be utilized to choose the preferred method based on the required accuracy and the available computational resources.

[6] T. Kadeetuhm, S.Lee, F. Ballarin, J. Choo, H.M. Nick A Locally Conservative Finite Element Framework for Coupled Hydro-Mechanical-Chemical Processes in Heterogeneous Porous Media, Volume 152, July 2021, 104774, Computers & Geoscinces
❀ Link to the journal
❀ Abstract: This paper presents a mixed finite element framework for coupled hydro-mechanical–chemical processes in heterogeneous porous media. The framework combines two types of locally conservative discretization schemes: (1) an enriched Galerkin method for reactive flow, and (2) a three-field mixed finite element method for coupled fluid flow and solid deformation. This combination ensures local mass conservation, which is critical to flow and transport in heterogeneous porous media, with a relatively affordable computational cost. A particular class of the framework is constructed for calcite precipitation/dissolution reactions, incorporating their nonlinear effects on the fluid viscosity and solid deformation. Linearization schemes and algorithms for solving the nonlinear algebraic system are also presented. Through numerical examples of various complexity, we demonstrate that the proposed framework is a robust and efficient computational method for simulation of reactive flow and transport in deformable porous media, even when the material properties are strongly heterogeneous and anisotropic.

Objective 2: Advanced Phase-Field Fracture Propagation

[7] S. Lee, M. F. Wheeler, Modeling interactions of natural and two phase fluid filled fracture propagation in porous media, Computational Geoscience, DOI: 10.1007/s10596-020-09975-0, 2020
❀ Link to the journal
❀ Abstract: In this paper, a novel computational framework is introduced for simulation of multiphase flow, geomechanics, and fracture propagation in porous media based on Biot's model for poroelasticity by focusing on interactions between hydraulic and natural fractures. Since realistic porous media contain many natural fractures, it is important not only to stimulate hydraulic fractures but also to study the interaction between natural and hydraulic fractures. Here, state-of-the-art numerical modeling of natural and hydraulic fractures using a diffusive adaptive finite element phase field approach is employed. The locally mass conservative enriched Galerkin finite element methods (EG) are utilized to model two-phase flow in propagating fractures with relative permeability and capillary pressure. Geomechanics approximated by a continuous Galerkin finite element method is coupled to multiphase flow by applying an iteratively coupled scheme. Numerical examples are presented that demonstrate the effectiveness of this framework for different propagation scenarios by varying the degrees of physics. In addition, the capabilities to perform high-fidelity simulations on complex fracture networks, with randomly joined diffusive natural fractures, are illustrated.
➪ Highlights :
  • This paper introduces natural fractures by utilizing the diffusive phase-field approach
  • The interactions between natural fractures and two-phase hydraulic fractures are demonstrated
  • Extension of pressure and width analyses, flowback effects, and the prodcution stage examples are considered
  • The below figures show some examples of the fractures in this paper


[8] M.F. Wheeler, T. Wick, S. Lee IPACS: Integrated Phase-Field Advanced Crack Propagation Simulator. An adaptive, parallel, physics-based-discretization phase-field framework for fracture propagation in porous media, Computer Methods in Applied Mechanics and Engineering, Volume 367, 1 August 2020, 113124
❀ Link to the journal
❀ Abstract: In this work, we review and describe our computational framework for solving multiphysics phase-field fracture problems in porous media. Therein, the following five coupled nonlinear physical models are addressed: displacements (geo-mechanics), a phase-field variable to indicate the fracture position, a pressure equation (to describe flow), a proppant concentration equation, and/or a saturation equation for two-phase fracture flow, and finally a finite element crack width problem. The overall coupled problem is solved with a staggered solution approach, known in subsurface modeling as the fixed-stress iteration. A main focus is on physics-based discretizations. Galerkin finite elements are employed for the displacement-phase-field system and the crack width problem. Enriched Galerkin formulations are used for the pressure equation. Further enrichments using entropy-vanishing viscosity are employed for the proppant and/or saturation equations. A robust and efficient quasi-monolithic semi-smooth Newton solver, local mesh adaptivity, and parallel implementations allow for competitive timings in terms of the computational cost. Our framework can treat two- and three-dimensional realistic field and laboratory examples. The resulting program is an in-house code named IPACS (Integrated Phase-field Advanced Crack Propagation Simulator) and is based on the finite element library deal.II. Representative numerical examples are included in this document.
➪ Highlights :
  • A software framework IPACS to simulate multiphysics phase-field fracture propagation in porous media.
  • Physics-based finite element discretizations and solvers for the coupled system
  • Iterative coupling methods and linear solvers.
  • Various applications considering realistic scenarios from laboratory scales to field scales.



Objective 3: Nonlinear Strain Limiting Coupeld with Phase-Field Fracture Propagation

[9] S. Lee, S.M. Mallikarjunaiah, H. Yoon, Nonlinear strain-limiting Elasticity for Fracture Propagation with Phase-Field Approach, Submitted 2020
❀ Abstract The conventional model governing the spread of fractures in elastic material is formulated by coupling linear elasticity with deformation systems. The classical linear elastic fracture mechanics (LEFM) model is derived based on the assumption of small strain values. However, since the strain values in the model are linearly proportional to the stress values, the strain value can be large if the stress value increases. Thus this results in the contradiction of the assumption to LEFM and it is one of the major disadvantages of the model. In particular, this singular behavior of the strain values is often observed especially near the crack-tip, and it may not accurately predict realistic phenomena. Thus, we investigate the framework of a new class of theoretical model, which is known as the nonlinear strain-limiting model. The advantage of the nonlinear strain-limiting models over LEFM is that the strain value remains bounded even if the stress value tends to the infinity. This is achieved by assuming the nonlinear relation between the strain and stress in the derivation of the model. Moreover, we consider the quasi-static fracture propagation by coupling with the phase-field approach to present the effectiveness of the proposed strain-limiting model. Several numerical examples to evaluate and validate the performance of the new model and algorithms are presented. Detailed comparisons of the strain values, fracture energy, and fracture propagation speed between nonlinear strain-limiting model and LEFM for the quasi-static fracture propagation are discussed.
➪ Highlights :
  • The novel nonlinear strain-limiting elasticity for quasi-static fracture propagation with phase-field approach is established, where the elasticity model is given as
  • The outcomes clearly shows the expected strain-limiting effects near the fracture tip where the stress values are large
  • The several numerical experiments to investigate the choice of nonlinear parameters are shown
  • The below figure illustrates the values of the strain near in the fracture. We observe the small strain values with the nonlinear strain limiting parameters.

[10] H.Yoon, S. Lee, S.M. Mallikarjunaiah, Quasi-Static Anti-Plane Shear Crack Propagation in a New Class of Nonlinear Strain-Limiting Elastic Solids using Phase-Field Regularization, Submitted 2020
❀ Link to the arXiv
❀ Abstract We present a novel constitutive model using the framework of strain-limiting theories of elasticity for an evolution of quasi-static anti-plane fracture. The classical linear elastic fracture mechanics (LEFM), with conventional linear relationship between stress and strain, has a well documented inconsistency through which it predicts a singular crack- tip strain. This clearly violates the basic tenant of the theory which is a first order approximation to finite elasticity. To overcome the issue, we investigate a new class of material models which predicts uniform and bounded strain throughout the body. The nonlinear model allows the strain value to remain small even if the stress value tends to infinity, which is achieved by an implicit relationship between stress and strain. A major objective of this paper is to couple a nonlinear bulk energy with diffusive crack employing the phase-field approach. Towards that end, an iterative L-scheme is employed and the numerical model is augmented with a penalization technique to accommodate irreversibility of crack. Several numerical experiments are presented to illustrate the capability and the performance of the proposed framework We observe the naturally bounded strain in the neighborhood of the crack-tip, leading to different bulk and crack energies for fracture propagation.
➪ Highlights :
  • The anti-plane shear fracture propagation in the class of nonlinear strain-limiting theories are developed
  • The Airy-stress varaibles are utilized
  • Compared to [9] more freedom on the choice of nonlinear parameters are provided
  • The below figure (Left) illustrate the phase-field values during crack evolution for each timestep, and (Right) presents the corresponding strain values for each case.


Confernece Presentations

● Sep 20 2019. Applied Math Seminar Department of Mathematics Auburn University Auburn, AL, USA

● Mar 14-15th 2020. 29th The Center for Subsurface Modeling Affiliates Meeting, The Oden Institute of CES, The University of Texas at Austin ● [14th-15th Mar 2020] The 44th SIAM Southeastern Atlantic Section Conference (link), Auburn University, USA

● [11th-13th May 2020] The 50th John H. Barrett Memorial Lectures, A3N2M: Approximation, Applications, and Analysis of Nonlocal, Nonlinear Models, (link), The University of Tennessee, Knoxville, USA

● [21st-25th Jun 2020] Computational Methods in Water Resources XXIII (CMWR) 2020 (link), Stanford University, USA

● [19th-24th July 2020] WCCM & ECCOMAS Congress 2020, Paris, France (link)

● [31st May - 4th June 2021] InterPore (link) 2021

● [7th-11thh June 2021] 13th International Conference on Large-Scale Scientific Computationse (link) 2021, Sozopol, Bulgaria

● [21st - 24th June 2021] SIAM Conference on Mathematical & Computational Issues in the Geosciences (GS21) (link), Politecnico di Milano, Milano, Italy

● [25th - 29th July 2021] 16th U.S. National Congress on Computational Mechanics, (link), Chicago, Illinois, USA




The Math Fun Day Event

The Department of Mathematics annually hosts FSU Math Fun, a joint Open House for the general public, including K-12 students and teachers. Come join us for some math fun! There will be lots of hands-on activities, presentations, exhibits, demonstration, and workshops. Activities are available for all ages in grades K-12, but students in kindergarten and grade 1 will need extra parental help. Anyone and everyone is invited to attend and all the activities are free.
Click for more information!


The Code for NonLinar Starin Limiting Fracture Propagation

  • The code is based on c++ deal.II finite element libraries

  • The license: This developed program is free software, which one can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. In addition, this program is distributed in the hope that it will be useful, but without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose. See the GNU General Public License for more details.

  • The code version 1 is still under development... the code will be shared by GitHub repository upon the request