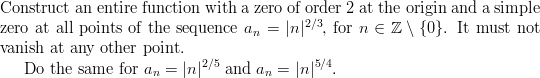Problems are not collected for grading, however you are supposed and expected to work out the problems on your own, without looking at the available solutions, if possible, and discuss them with me, or ask about them in class.
Homework & Notes
-
Problem on normal families
(PDF here):
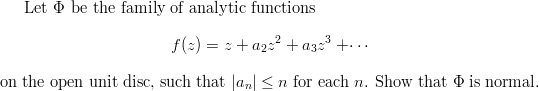
-
Consider the remark on page 231 of Stein, after the
proof of the Riemann mapping theorem, and the discussion of
simple connectivity in Appendix B:
- Can you replace the assumption that Ω be simply connected with only that log f(z) exists?
- If you define "log-simply connected" to mean that log f(z) exists for every holomorphic function f(z), then is this equivalent to the usual notion of simple connectivity?
- Problem 4, Chapter 8, of Stein (in the Problems section, so it's the one on page 257).
-
Problem on automorphism groups
(PDF here):
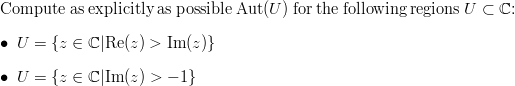
- Problem 2C, page 53 of Jones & Singerman.
- Prove there are no loxodromic elements in the automorphism group of the unit disc.
-
Problem on harmonic functions
(PDF here):
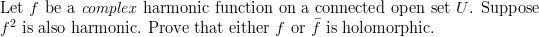
- Use a change of variable and an appropriate conformal map to establish a Poisson formula on the upper half plane.
-
Problem on harmonic functions
(PDF here):
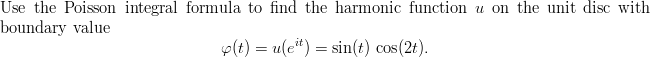
-
Problem on analytic continuation:
(PDF here):

-
Another problem on analytic continuation:
(PDF here):

-
One more problem on analytic continuation:
(PDF here):

-
Problem on estimates:
(PDF here):
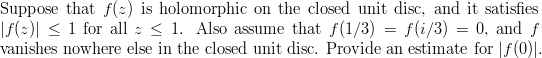
-
Use what you know about infinite products and sums
(PDF here):

-
Problem on entire functions
(PDF here):