| Course page: |
ON CAMPUS: http://www.math.fsu.edu/~mesterto/MGF3301.html (this
page)
OFF CAMPUS:
http://www.math.fsu.edu.proxy.lib.fsu.edu/~mesterto/MGF3301.html
(with your FSUID username and password) |
| Professor: | Dr Mesterton-Gibbons, or Dr M-G for short |
| Office: | 202B Love
|
| Office hours: |
Please click here. Office hours are
subject to change during the semester at 24 hours notice, but
current times are always posted online. Note that office hours are
primarily for personal matters that cannot be addressed in class
(as opposed to tutorial help, for which see under How to study below) |
| Phone: | (850 64) 42580
|
| Main website: |
Professor M-G's
Home Page Email: |
| Goal: | To
introduce the methods of mathematics through a variety
of classical and modern topics. Axioms and proofs will
be emphasized throughout |
| Class meets: |
In 106 LOV on Mondays, Wednesdays and Fridays at
10:10—11:00 a.m. |
| Text: | Krantz, Elements of Advanced
Mathematics, 3rd edition (CRC Press, 2012; ISBN 978-1-4398-9834-5
Hardback, 978-1-4398-9843-7 eBook). We will cover most (but not all)
of Chapters 1-4 and 6, and a selection of material from other
chapters and elsewhere |
| Credit: | 3 semester hours |
| Eligibility: | You must have the prerequisites
listed below, and you must not have credit for MAD 2104
Discrete Mathematics I, MAA 4224 Introduction to Analysis, MAS 4302
Introduction to Abstract Algebra, MAA 4226 Advanced Calculus I or
their equivalents. |
| Prerequisites: |
| (i) |
MAC 2312 Calculus II and |
| (ii) |
self-motivation and industriousness and |
| (iii) |
the patience to believe in yourself—you may not get
it right away, but given (ii), if you are patient, then
understanding will come |
| My philosophy of learning is perhaps best expressed
by the green curve in the diagram below: |
|
| |
ALTERNATIVE THEORIES OF LEARNING VERSUS
PAIN
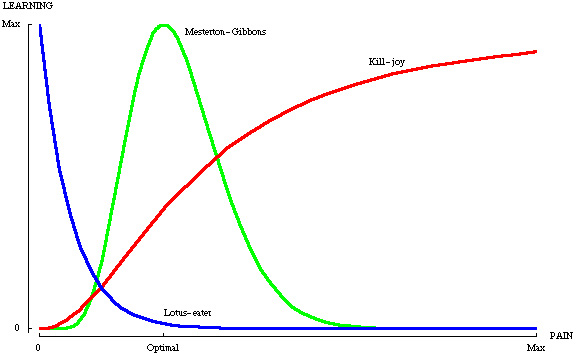 |
For further details, please click here.
|
| Communication: |
I will send email to your FSU email account on a regular
basis. It is your responsibility to check it regularly (or arrange to
have my messages forwarded, if you prefer to read your email
elsewhere) |
| Your name: |
 |
| I don't
know who you are (for the most part), but because everything
works so much better when I do, I would like to learn your name
as soon as possible. So, please take a sheet of card stock (or
even paper), fold it in half, write your name in large letters
on one side and stand it up on your desk so that I can see it.
(Write what you want me to call you: if you're a William who
likes to be called Dubya or a Margaret Jane who likes to be
called Dee Dee, write Dubya or Dee Dee, not William or Margaret
Jane.) Please bring your nameplate to every class until I have
finally learnt your name (which will take significantly longer
than it used to take when I started out) |
|
| Course format: | The course will
be based on my lectures, your reading of the text and other materials
(supplied by me) and much interactive problem solving—on which we plan
to spend most of our time in class. After each period I will set
homework for the following period, either at the end of class or soon
afterwards by email. This homework will consist of one or more of the
following:
- Exercises on the current topic or topics
- An assigned reading, typically on the next topic(s), hence
typically the next section or two of the text
- A problem or problems associated with the assigned
reading
At the start of each class, I will always assume that you have both
read (though not necessarily fully understood) any assigned reading and
at least seriously attempted (though not necessarily completed) any
associated problem(s). I will also assume that you are going to
complete Item 1 in a timely fashion, though not necessarily in full by
the following period.
Typically, we will begin class by reviewing up
to three different solution attempts that you have written on the
board. A lecture will often follow. Early in the semester, that
lecture will tend to be very brief. Its purpose will be to highlight
the key points of an assigned reading, largely to jog your memory of
reading it earlier, perhaps also partly to add some fresh
perspective—but in any event based on the assumption that you
have actually read it. As the semester progresses, however,
lectures are likely to lengthen, because I will introduce material not
covered by the text. Either way, I will work from notes that get
posted here as soon after class
as I can manage.
We will then proceed to work on problems,
beginning with Item 3 if there exists an Item 3. Note the use of
we—interactive problem solving implies working together,
and in this class your active participation is vital. To encourage you
in that regard, 15% of your final grade will be based on the extent to
which you have participated in class.
In particular, on any given class day, up to
three of you can earn 3% of your grade by writing a sufficient attempt
at a homework problem on the board immediately before class. You must
clear your choice of problem beforehand with me. I will then notify
the class that the problem is taken, and up to two more of you can pick
a different problem. The rest of you will have to wait for a later
class. There are 37 non-test periods after the first, yielding
capacity for 111 sufficient attempts; the enrollment is 22 and 5 x 22 =
110 < 111, so all of you in principle can earn all your participation
points this way. But you can also earn them in class in other
ways—by asking very good questions, by exemplary contributions to
interactive problem solving, etc., etc. (where "etc., etc." just
means whatever other ways I might have overlooked).
Questions may be asked at any time—and should be, if
there's anything you don't understand. (Perhaps you have a question
about the assigned reading that you anticipate being answered by one or
more of the problems we work together; in which case, it may well be
socially minded not to ask your question at the outset. However, if it
turns out that you anticipated incorrectly, then be sure to ask your
question before the class is over!) |
| Test format: | You must write your answers in blue
or black ink. If you make a mistake, then just cross it out and
make a correction, which is far more efficient temporally than erasing
pencilling—moreover, it can even earn you otherwise unavailable
partial credit (if it turns out that you were right before you changed
your mind). Begin each question (but not subsequent parts of the same
question) on a fresh sheet of paper, use one side of the paper only,
and have your solutions stapled together in order at the end of the
examination (without the question sheet, which is yours to keep).
Please do not use dog ears (I will bring a stapler to the
classroom). Needless to say, your name must appear legibly on Page 1
of your solutions (as opposed to on the question sheet, which will not
help, because you are keeping it) |
| Grades: | Will be based on participation in
class (15%), four tests (15% apiece) and a cumulative final exam (25%),
for all of which you must use blue
or black ink.
Precise cut-off points for A, B and C will be
determined by the distribution of grades at the end of the semester,
but are likely be in the vicinity of 90%, 80% and 70%, respectively.
In borderline cases, a smaller number of perfect answers will carry
more weight than a proportionate number of imperfect answers (e.g., a
ten and a zero will trump two fives); later scores will carry more
weight than earlier scores; and—above all—an exemplary
record of class participation will carry far more weight than a
mediocre one. Plus or minus grades may be assigned in a manner
consistent with standard University practice.
A score for a question worth 10 points should
be interpreted as follows:
| 10 |
Practically perfect |
9 |
Still very good, but
lacking—or wrong about—a significant detail |
| 8 |
Still good, but lacking—or
wrong about—significant details |
| 7 |
Minimally satisfactory. You
have—just—managed to demonstrate that you basically
understand and are at least capable of getting all details correct
(although it clearly did not happen this time) |
| 6 |
A grade that will not be given |
| 5 |
Half right in some appropriate sense
(e.g., there were two parts, each worth 5 points, and your first part
was practically perfect) |
| 1-4 |
Not even half right and showing
little understanding, but some degree of positive effort |
| 0 |
Zero effort, or submitted in pencil |
Also note that a grade of I will not be given to avoid a grade of F or to
give additional study time. Failure to process a course drop will result
in a course grade of F |
| Solutions to homework problems: | Will eventually be
posted here. I caution you, however: never
read a posted solution until first of all you have seriously
attempted the problem yourself. If you have at least made a serious
attempt, then even if you were unable to complete the problem yourself,
you will benefit from reading the posted solution; if not, then
not—rather, you will merely form a false impression of how well
you understand ... as indicated by the above learning-versus-pain diagram. To help you in this
regard, solutions will be posted only after a significant delay |
| Test solutions: |
Will be posted here |
| Attendance policy: | You are expected to
attend class regularly, and bear the full responsibility for learning
anything covered during any class that you miss. On the other hand, it
would be extremely anti-social to attend class if you either have, or
are coming down with, a contagious disease. So please keep me apprised
(by email) of any illness or other emergency, so that I can make any
necessary adjustments (and please make friends within the class as soon
as possible if you haven't done so already, so that there is someone
you can call upon to borrow notes if the need should arise) |
| Exam policy: | No makeup exams. An absence may be
excused given sufficient evidence of extenuating circumstances (in
which case, extra weight will be attached to the other exams or—if
necessary, and only if necessary—an oral exam may be substituted).
But you must either have discussed the matter with me (well) in
advance; or, e.g., in the case of illness, have brought me a note from
a physician explicitly stating that you were too ill to attend class on
the day in question. An unexcused absence will result in a grade of
zero |
| Etiquette: | You are firmly bound by Florida State
University's Academic Honor Code. Briefly,
you have the responsibility to uphold the highest standards of academic
integrity in your own work, to refuse to tolerate violations of
academic integrity in the University community, and to foster a high
sense of integrity and social responsibility on the part of the
University community. Even more briefly, you must neither cheat nor
enable others to cheat. The penalties for violations can be severe.
Please carefully read the section in the FSU Student Handbook on the
Honor Code and official procedures for dealing with students who
violate it. If you are in any doubt at all as to what constitutes
acceptable behavior in this regard, you should ask me for
clarification.
You are also bound by the ordinary rules and
customs of polite behavior that prevail in a civilized society. I
assume that you know these rules and customs, and I expect you to
comply with them. (In particular, you are not allowed to use a cell
phone or otherwise have private conversations with others during class;
and you are not allowed to create disturbances through arriving late or
leaving early.) |
| Probable test dates: |
Monday, February 01
Monday, February 22
Monday, March 28
Monday, April 11 |
| Final: | Thursday, April 28, 10:00
a.m.—12:00 noon in 106 LOV |
| How to study: | It is
important that you keep up with the course from the very beginning,
always attempting as many as possible (preferably all) of the homework
exercises. If you get stuck, then send me a question by email. As
soon as I possibly can, which might be as soon as within half an hour,
but might also be a day or two later (I have a life, too, you know), I
will reply—not to you, but rather to the class alias (after
carefully concealing your identity, just in case you are inexplicably
bashful about being perceived as smart enough to ask a question). My
reply will aim at nudging you over the immediate hurdle so that you can
then take the next step by yourself (as opposed to supplying a complete
solution, again for reasons encapsulated by the above learning-versus-pain diagram).
Note, however, the following. First, you must
identify yourself (i.e., you remain anonymous to the other students in
the class, but not to me) in the body of your message (because
typically your username does not identify you to me): I don't reply to
anonymous email. Second, you should be as specific as possible in
describing your difficulty: the more precisely you identify how you got
stuck, the more helpful my reply is likely to be. |
| Disabilities: | If you have a disability requiring
academic accommodations, then not only should you register with the Student
Disability Resource Center (SDRC),
but also you should bring me written confirmation from SDRC during the
first week of class. This and other class materials are available in
alternative format upon request. |
This syllabus and other class materials are available in alternative format
upon request.
For more information about services available to FSU students with
disabilities, contact the:
On-campus tutoring and writing assistance is available for many courses at
Florida State University. For more information, visit the Academic Center
for Excellence (ACE) Tutoring Services' comprehensive list of on-campus
tutoring options—see http://ace.fsu.edu/tutoring or contact tutor@fsu.edu. High-quality
tutoring is available by appointment and on a walk-in basis. These
services are offered by tutors trained to encourage the highest level of
individual academic success while upholding personal academic integrity.
"Except for changes that substantially affect implementation of the
evaluation (grading) statement, this syllabus is a guide for the course and
is subject to change with advance notice.''

