Teaching Philosophy

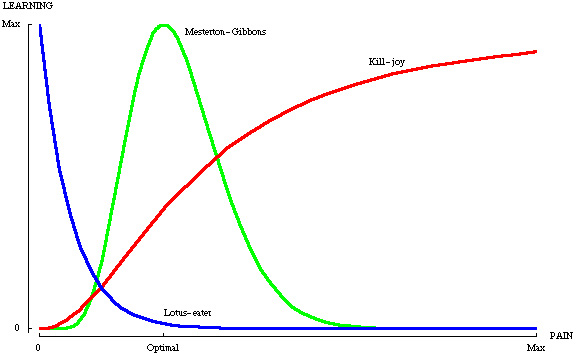
On the time scale of any given semester, my objective as teacher is to maximize learning subject to inevitable populational constraints. My strategy for attaining it is adaptive: every class has its unique collective personality, and the best way to deal with it varies from semester to semester. My teaching philosophy is perhaps best expressed by the above diagram, with which I like to confront my students at the start of every course.
     I believe that how to learn is the most important lesson to learn from one's academic studies, and that one can grow confident in one's ability to study independently only by being challenged to explore it. I like students to think of me as a facilitator, and I dislike the word "instructor"—it suggests that knowledge can be unilaterally imparted. On the contrary, education is a cooperation between teacher and students, who must be respected as adults and expected to act accordingly. My duties in this cooperation include motivating and introducing the subject; helping students to learn the subject, by responding to their difficulties in reading the text and by solving problems interactively with them in class; and monitoring and grading their progress. The students' duties include doing their homework, reviewing adequately for tests, and providing necessary feedback by asking or answering questions in class.
     According to Robert Axelrod (The Evolution of Cooperation, Basic Books, New York, 1984), a good cooperative strategy should be simple, nice and forgiving, but provocable. My teaching strategy is simple, because classes are a predictable assemblage of matters arising from homework, short lectures on new material, much problem solving, questions (in either direction) and answers, and assignment of homework for the following period. My strategy is nice, because I strive to conduce learning by maintaining a good-natured atmosphere in class, and because students know what is expected of them. My strategy is forgiving, because in borderline cases later test scores carry more weight than earlier ones. But my strategy is also provocable, because if students fail to cooperate, then they also fail my course.
     On the longer time scale of my twenty five years at FSU, a major teaching objective has been to make mathematics more attractive to students by incorporating modern applications into the undergraduate curriculum. In particular, I completely revamped an existing 4000-level course on modelling (MAP 4103, Mathematical Modelling) to emphasize applications of mathematics in the life, management and social sciences; and I introduced a brand new 4000-level course on game theory (MAP 4180, Game Theory and Applications).
     My efforts in this regard have earned me international recognition as a teacher, largely as a result of two innovative books, A Concrete Approach to Mathematical Modelling (Addison-Wesley, 1989; Wiley, 1995, 2007) and An Introduction to Game-Theoretic Modelling (Addison-Wesley, 1992; American Mathematical Society, 2001). Reviewers said of the first:

There is a wealth of ideas here for lecturers, both in how to present material, and for examination questions; and the persistent attempt to enliven the work by providing real practical contexts is most refreshing. ... This book is a treasure-house of material for students and teachers alike, and can be dipped into regularly for inspiration and ideas. It deserves to become a classic.     London Times Higher Education Supplement

A tremendous amount of hard labour must have gone into the preparation of this interesting book. ... Balancing between a methodological and an example-oriented approach, the author seems to have found the way to structure an in-depth course on mathematical modelling in such a way that students will have to like it.     Short Book Reviews

The author certainly takes the student carefully through the model building process. ... Each chapter discusses a wealth of examples ... Each model is developed critically, analyzed critically, and assessed critically.     Mathematical Reviews

The author succeeds in his goal of serving the needs of the undergraduate population who want to see mathematics in action, and the mathematics used is extensive and provoking.     SIAM Review of Applied Mathematics

It shows how all the basic first two years of undergraduate math is really useful, and...students see that they can... learn new math as necessary for the problem at hand. It has an emphasis on testing and evaluating models. ... Few books emphasize that good applied math is also good science, and Mesterton-Gibbons is one that does.     UME Trends

Reviewers said of the first edition of the second book:

I find this book excellent and I think it is worth considering it when teaching an undergraduate course in game theory to students having some mathematical maturity (some calculus, some knowledge of matrix analysis and probability).     Zentralblatt für Mathematik

Each chapter is supported by numerous carefully chosen exercises as well as answers to selected exercises. The exercises support understanding the modeling process ... The book has been written such that it is suitable for teaching purposes, either as a lecture series or as a seminar. ... The number of books about game theory modeling are not too many due to the obvious problems of teaching mathematical modeling. ... In this book the author has made a courageous choice, and I appreciate the result.     Natural Resource Modeling

... the reader is taken from introductory material to the "cutting-edge" ...      Bulletin of Mathematical Biology

Readers will be hard-pressed to find a general introduction to game theory that blends biological and mathematical approaches more expertly. It is both a well-rounded survey, and a reference work of lasting value.      Behavioral Ecology

Reviewers said of the second edition of the second book:

The mathematics described in Mesterton-Gibbons' book is fascinating, and well worth studying for its own sake even if one doesn't care about mathematical modelling. ... One of the book's strengths is that it analyzes interesting examples, rather than artificial examples chosen to take only one page. ... This book's examples fill the sad gap between the single-step problems one solves in calculus textbooks and the multi-step problems one faces in real life. ... I know of nothing like it as a collection of illuminating examples. Everyone interested in game theory or mathematical modelling should take a look at it.      MAA Online Reviews

I enjoyed this book, and will value it as a reference. Mesterton-Gibbons has written a remarkable instructional guide to both games and a quantitative theory for social behavior. The book motivated me to take up some research questions I had dropped a few years ago. Anyone intested in the adaptive evolution of behaviour should read this book; anyone intent on developing a skill in modelling social interactions will want a copy.     Animal Behaviour

A third book appeared in 2009. Reviewers of A Primer on the Calculus of Variations and Optimal Control Theory have said:

... the author clearly understands the pedagogical challenge of teaching to the advanced undergraduate mathematics audience, has done an excellent job of delivering a treatment of Calculus of Variations and Optimal Control to this audience. The text is clear and readable, and sufficiently rigorous.     Advance Review

This book achieves exactly what it sets out to do: It gives a thorough introduction to the topics given in its title, with minimal prerequisites. ... From a mathematical point of view, it is a good book, especially useful for undergraduates and beginning graduate students.     MAA Online Reviews