MAD 3105, Section 01, Fall 2007
(Reference #02317 in
Directory of Classes)
| Professor: | Dr M-G | ||||
| Office: | 202B Love | ||||
| Office hours: | Please check here, where current times are always posted. Office hours are subject to change during the semester at 24 hours notice (in principle, though rarely in practice). Note that office hours are primarily for personal matters that cannot be addressed in class (as opposed to tutorial help, for which see How to study) | ||||
| Phone: | (850 64) 42580 | ||||
| Email: | mesterto@math.fsu.edu | ||||
| Web site: | http://www.math.fsu.edu/~mesterto | ||||
| Goal: | The purpose of this course is to develop knowledge and skills in fundamental mathematical topics—in particular, relations, graphs and Boolean algebra—that are relevant to computing, especially to the systematic development of software. The course is a requirement of the computer science major. (Click here to download an important message from the Chair of Computer Science—addressed to all students of discrete mathematics, and hence to you—on the importance of this very topic.) | ||||
| Course page: | http://www.math.fsu.edu/~mesterto/DiscreteMathII.html (this page—but obviously, if you are reading a hard copy of it, then you won't be able to activate the links until you go online) | ||||
| Class meets: | 2:00 p.m.—3:15 p.m., Tuesdays
and Thursdays in 102 LOV |
||||
| Text: | Kenneth H Rosen, Discrete
Mathematics and its
Applications, 6th edition (McGraw Hill,
2007, ISBN:
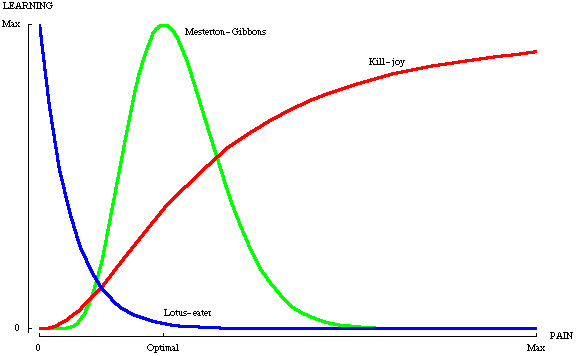
978-0-07-288008-3). Selected topics from Chapters 8-11. Recommended supplementary text: the accompanying student solutions guide (ISBN: 978-0-07-310779-0). I caution you, however: never read a solution to a problem until first of all you have seriously attempted the problem yourself. If you have at least made a serious (and I do mean serious) attempt, then—even if you were unable to complete the problem yourself—you will benefit from reading the guide's solution to it; if not, then not (rather, you will merely form a false impression of how well you understand ... as indicated by the diagram below). Needless to say, this advice also applies to solutions I post online. |
||||
| Credit: | 3 semester hours | ||||
| Eligibility: | Is your responsibility. You must have the prerequisites listed below, and must never have completed with a grade of C- or better a course for which MAD 3105 is a (stated or implied) prerequisite | ||||
| Prerequisites: |
|
||||
|
|||||
| Communication: | It is your responsibility to register here for a (free) FSU computer account so that I can send you email, which you are expected to check regularly. If you prefer to read your email elsewhere then you can arrange to have messages forwarded, but you must still obtain an FSU account in the first instance | ||||
| Your name: |
|
||||
| Course Format: | We will follow the text, spending most of
our time in class on
solving problems. At the end of each period
I will set homework for the
following period (if not immediately
in class, then soon afterwards by
email). Typically, this
homework will consist of a set of further
problems on the topic
we have just studied together with a passage of
text to be read
for the following period; for example, your homework
for
Thursday, August 30 is to do as many as possible of Exercises 1,
3, 19, 21, 23, 25 and 27 on Pages 542-544 and to read Section 8.1 (we
will
broach Section 8.3—out of sequence—on August 28
because, for
the most part, it doesn't require Section 8.1). In
class, I will always
assume that you have read (though not
necessarily understood) the
assigned passage. A typical class will then proceed as follows. It will begin with an opportunity for you to ask questions about the homework problems. Depending on the time available, I will answer each question either in class or (especially if an even-numbered problem is involved) by posting a solution online later, or by some combination of the two. We will then move on to the topic of the current period. I will give a brief lecture summarizing the key points of the passage you have read for homework—enough to get us going, but deliberately excluding details—before proceeding as quickly as possible to solving problems (in which the details will emerge), with as much interaction as possible from you. Questions may be asked at any time—and should be, if there's anything you don't understand. (Perhaps you have a question about the assigned reading that you anticipate being answered by one or more of the problems we work together; in which case, it may well be socially minded not to ask your question at the outset. However, if it turns out that you anticipated incorrectly, then be sure to ask your question before the class is over!) |
||||
| Test Format: | Begin each question (but not subsequent parts of the same question) on a fresh sheet of paper, use one side of the paper only, and have your solutions stapled together in order at the end of the examination (do NOT use dog ears). Not owning a stapler is no excuse: I will bring a stapler to the final, and for the tests you can borrow the stapler in 208 Love. Needless to say, your name must appear legibly on the first page | ||||
| Grades: | Will be based on three take-home
tests (24% each) and a cumulative
final examination (28%). Each
test will begin at the end of
class on a Tuesday (see
below) and end at the beginning of class
on the Thursday
immediately following. Note that quality of presentation is extremely important. It is not enough merely to produce an answer: the method by which you obtain it must be sound, and you must clearly demonstrate that you understand it. Therefore, there will be penalties (commensurate with degree of infraction) for bad presentation—which includes bad grammar, illegibility, incompleteness, incoherence and untidiness—especially on the take-home tests. Even on the final, however, you must show all necessary steps in your method, with enough comments and/or diagrams to convince me that you thoroughly understand. Precise cut-off points for A, B and C will be determined by the distribution of grades at the end of the semester, but are likely be in the vicinity of 90%, 80% and 70%, respectively. In borderline cases, later scores will carry more weight than earlier scores; a smaller number of completely correct solutions will carry more weight than a proportionate number of fragmentary answers; and a record of active participation in class will carry more weight than a record of passive attendance (in that order of relative importance among these three factors). Plus or minus grades may be assigned in a manner consistent with standard University practice. Please note that partial credit will be awarded only when part of a solution is completely correct (not when all of a solution is partially correct, whatever that means, if anything). Also, a grade of I will not be given to avoid a grade of F or to give additional study time. Failure to process a course drop will result in a course grade of F |
||||
| Test solutions: | Will be posted online here (along with the test itself), making grading more efficient: instead of writing the same corrections on numerous manuscripts, I simply identify the point(s) at which a solution goes awry | ||||
| Attendance policy: | You are expected to attend class regularly, and bear the full responsibility for learning anything covered during any class that you miss | ||||
| Exam policy: | No makeup exams. An absence may be excused given sufficient evidence of extenuating circumstances (in which case, extra weight will be attached to the other exams). But you must either have discussed the matter with me (well) in advance; or, in the case of illness, have brought me a note from a physician explicitly stating that you were too ill on the date(s) in question. An unexcused absence will result in a grade of zero | ||||
| Etiquette: | You are firmly
bound by Florida State University's Academic Honor Code. Briefly, you have the
responsibility to uphold the highest standards of academic integrity
in
your own work, to refuse to tolerate violations of academic
integrity
in the University community, and to foster a high
sense of integrity
and social responsibility on the part of the
University community. Even
more briefly, you must neither cheat
nor enable others to cheat. The
penalties for violations can be
severe. Please carefully read the
section in the FSU Student
Handbook on the Honor Code and official
procedures for dealing
with students who violate it. If you are in any
doubt at all as
to what constitutes acceptable behavior in this regard,
you
should ask me for clarification. In particular, for a take-home test you may use any inanimate aid (including any calculator), but all such use must be explicitly declared. Although you may discuss the test with other students in general terms—meaning that discussion is oral, and absolutely nothing is copied down—the solutions you present must be your very own work; moreover, any such discussions must be explicitly declared (i.e., you must supply the name of every such discussant and the nature of the discussion, or else you are in violation of the Academic Honor Code). You are also bound by the ordinary rules and customs of polite behavior that prevail in a civilized society. I assume that you know these rules and customs, and I expect you to comply with them. (In particular, you are not allowed to use a cell phone or have private conversations with others during class.) |
||||
| Probable test dates: | Tuesday, September
25 (due Thursday, September 27) Tuesday, October 23 (due Thursday, October 25) Tuesday, November 27 (due Thursday, November 29) |
||||
| Final: | Friday, December 14, 3:00—5:00 p.m. in 102 LOV | ||||
| How to study: | There is a lot of material to be
covered in this course, so it is
important that you keep up from
the very beginning, always attempting
as many as possible (or as
necessary) of the homework problems. If you
get stuck, then send
me a question by email. As soon as I possibly can,
which might be
as soon as within half an hour, but might also be a day
or two
later (I have a life, too, you know), I will reply—not to
you, but rather to the class alias (after carefully concealing your
identity, just in case you are inexplicably bashful about being
perceived as smart enough to ask a question). Often I will attach a
PDF
file to my reply. If you can't open it, then I can't help
you, because
the problem is at your end (you may not have the
latest version of
Adobe Reader, available here);
and so you must either fix it (with help from University Computing Services,
if
necessary) or download the file from here
instead. Note, however, the following. First, you must identify yourself (i.e., you remain anonymous to the other students in the class, but not to me) in the body of your message (because your username does not identify you to me): I don't reply to anonymous email. Second, you should be as specific as possible in describing your difficulty: the more precisely you identify how you got stuck, the more helpful my reply is likely to be. |
||||
| Disabilities: | If you have a disability requiring academic accommodations, then not only should you register with the Student Disability Resource Center (SDRC), but also you should bring me written confirmation from SDRC during the first week of class. This and other class materials are available in alternative format upon request. |
Supplementary Materials
Posted in PDF format. (You can view PDF files with
Adobe
Reader.)
Solutions to Problems
Posted in PDF format. (You can view PDF files with
Adobe
Reader.)
Solutions to Tests
Posted in PDF format. (You can view PDF files
with Adobe
Reader.)
| First Test | Solutions |
| Second Test | Solutions |
| Third Test | Solutions |
| Final | Solutions |
| Back to top of page | HOME | Back to top of page |