OFF CAMPUS: http://www.math.fsu.edu.proxy.lib.fsu.edu/~mesterto/ComplexVariables.html (with your FSUID username and password)
| (i) | C- or better in MAC 2313 (Calculus with Analytic Geometry III) and |
| (ii) | self-motivation and industriousness and |
| (iii) | the patience to believe in yourself—you may not get it right away, but given (ii), if you are patient, then understanding will come |
| My philosophy of learning is perhaps best expressed by the green curve in the diagram below: | |
ALTERNATIVE THEORIES OF LEARNING VERSUS
PAIN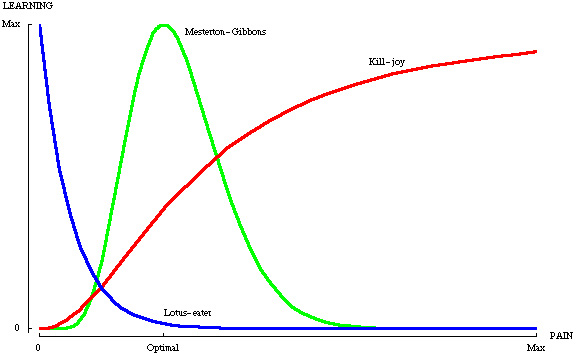 |
 |
I don't know who you are, but because everything works so much better when I do, I would like to learn your name as soon as possible. So, please take a sheet of card stock (or even paper), fold it in half, write your name in large letters on one side and stand it up on your desk so that I can see it. (Write what you want me to call you: if you're a William who likes to be called Dubya or a Margaret Jane who likes to be called Dee Dee, write Dubya or Dee Dee, not William or Margaret Jane.) Please bring your nameplate to every class until I have finally learnt your name (which will take significantly longer than it used to take when I started out) |
- Problems on the current topic or topics
- An assigned reading (not uncommonly the next few sections of the text, but we will sometimes skip sections or combine them in nonsequential order)
- A problem or problems associated with the topic or topics of the assigned reading
- Do:
From Exercises 2 (p. 5): ##1, 4 and as many as possible of the other problems (not already done in class)
From Exercises 3 (p. 8):##1a, 1b and as many as possible of the other problems
From Exercises 8 (p. 22):##1, 2, 5 and as many as possible of the others
Obviously, it gets tiresome to keep repeating ``as many as possible ...'' when it is always implied, so in setting homework I will abbreviate ``as many as possible ...'' to a simple ``etc.'' - Read §§4-5 (pp. 9-14) and if possible §11 (pp. 31-32), as well as §§6-8 (pp. 16-22) if you have not already done so
- At least seriously attempt #1 of Exercises 4 (p. 12) and #1 of Exercises 5 (p. 14)
We will then proceed to work on problems, beginning with Item 3. Questions may be asked at any time—and should be, if there's anything you don't understand. (Perhaps you have a question about the assigned reading that you anticipate being answered by one or more of the problems we work together; in which case, it may well be socially minded not to ask your question at the outset. However, if it turns out that you anticipated incorrectly, then be sure to ask your question before the class is over!)
On days when there is no quiz, we will attempt to end the formal class period after about an hour, so that the last 15-20 minutes or so can be devoted to individual tutorial help.
Homework, however, is an entirely different matter. For homework, you are not only allowed to use a graphing calculator or mathematical software, you are strongly encouraged to do so. The rationale behind this policy is as follows: You should use a graphing calculator or mathematical software only to speed up tasks you understand so well that you could carry them out flawlessly without the help of a graphing calculator or mathematical software, if you had sufficient time and did not have access to either tool. Tests are designed to assess whether you have attained the requisite level of understanding (and the time allowed will be commensurate).
Precise cut-off points for A, B and C will be determined by the distribution of grades at the end of the semester, but are likely be in the vicinity of 90%, 80% and 70%, respectively. In borderline cases, a smaller number of completely correct solutions will carry more weight than a proportionate number of fragmentary answers; later scores will carry more weight than earlier scores; and a record of active participation in class will carry more weight than a record of passive attendance. Plus or minus grades may be assigned in a manner consistent with standard University practice.
Please note that partial credit will be awarded only when part of a solution is completely correct—not when all of a solution is partially correct, whatever that means, if anything. A score for a question worth 10 points should be interpreted as follows:
| 10 | Practically perfect | 9 | Still very good, but lacking—or wrong about—a significant detail |
| 8 | Still good, but lacking—or wrong about—significant details |
| 7 | Minimally satisfactory. You have—just—managed to demonstrate that you basically understand and are at least capable of getting all details correct (although it clearly did not happen this time) |
| 6 | A grade that will not be given |
| 5 | Half right in some appropriate sense (e.g., there were two parts, each worth 5 points, and your first part was practically perfect) |
| 1-4 | Not even half right and showing little understanding, but some degree of positive effort |
homework exercises:
Will be posted here, but only if specifically requested (if you ask in class, be advised to back up your request with an email, otherwise I am likely to forget). I caution you, however: never read the posted solution to a problem until first of all you have seriously attempted the problem yourself. If you have at least made a serious (and I do mean serious) attempt, then—even if you were unable to complete the problem yourself—you will benefit from reading the posted solution; if not, then not (rather, you will merely form a false impression of how well you understand ... as indicated by the green curve in the above learning-versus-pain diagram)
You are also bound by the ordinary rules and customs of polite behavior that prevail in a civilized society. I assume that you know these rules and customs, and I expect you to comply with them. (In particular, you are not allowed to use a cell phone or otherwise have private conversations with others during class; and you are not allowed to create disturbances through arriving late or leaving early.)
Friday, July 20
Friday, August 03
Friday, July 27
Friday, August 10
Note, however, the following. First, you must identify yourself (i.e., you remain anonymous to the other students in the class, but not to me) in the body of your message (because your username does not identify you to me, and I don't reply to anonymous email). Second, you should be as specific as possible in describing your difficulty: the more precisely you identify how you got stuck, the more helpful my reply is likely to be.