| Professor: | Dr M-G
|
| Office: | 202B Love
|
| Office hours: |
Please check here, where
current times are always posted. Office hours are
subject to change during the semester at 24 hours
notice (in principle, but rarely in practice). Note
that office hours are primarily for personal matters
that cannot be addressed in class (as opposed to tutorial help, for which see Course format) |
| Phone: | (850 64) 42580
|
| Email: | mesterto@math.fsu.edu
|
| Web site: | http://www.math.fsu.edu/~mesterto |
| Goal: |
To introduce calculus, which is among the most broadly
applicable mathematics in existence |
| Course
page: | http://www.math.fsu.edu/~mesterto/CalcI.html (this
page—but
obviously, if you are reading a hard copy of it, then you won't be able to
activate the links until you go online) |
|
Class meets: |
Section 09: in 106 LOV, Mondays 02:30 — 03:20 p.m., Tuesdays and Thursdays
02:00 — 03:15 p.m.
Section 10: in 106 LOV, Mondays 03:35 — 04:25 p.m., Tuesdays and Thursdays
03:35 — 04:50 p.m.
|
| Text: |
Stewart, Calculus: Early Transcendentals, 5th edition
(Thomson, 2003, ISBN 0-534-39321-7), Chapters 2-6. Note that Chapter 1
contains only material that you already know, at least in principle.
Use it for reference whenever you need it, and don't be afraid to use
the index: it is easily the most important section of any mathematics
text. For example, if you can't remember what a polynomial is, don't
sit around moping—look it up in the index on p. A133, where you'll
be directed straight to p. 29. (As it happens, I will remind you what a
polynomial is in Lecture 2, but you get the idea.) |
| Credit: | 4 semester hours |
| Eligibility: |
Is your responsibility. You must have the prerequisites
listed below, and must never have completed with a grade of C- or
better a course for which MAC 2311 is a (stated or implied)
prerequisite. If you have prior credit in college calculus, you must
reduce the credit for MAC 2311 accordingly |
| |
ALTERNATIVE THEORIES OF LEARNING VERSUS
PAIN
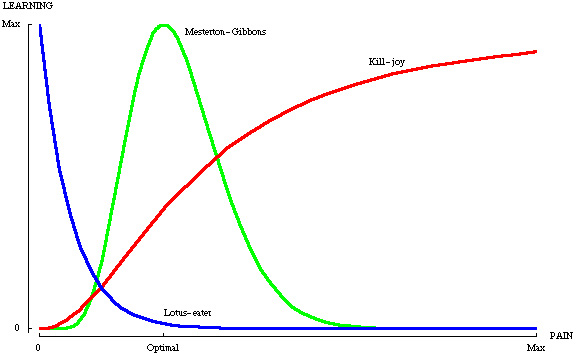 |
For further details, please click here.
|
| Prerequisites: |
| (i) |
C- or better in MAC 1114 (Analytic Trigonometry) and MAC 1140
(Precalculus Algebra) or in MAC 1147 (Precalculus
Algebra/Trigonometry) at FSU, or in MAC 2140 and MAC 1114 at TCC;
or appropriate transfer credit; or placement in AMP Group 1 or 1H
(or 2 if you are currently taking trigonometry); or AMP Group 3A
with prior college algebra; or AMP Group 3B with prior college
trigonometry and |
| (ii) |
self-motivation and industriousness. Dr M-G's philosophy of
learning is perhaps best expressed by the theory-of-learning
diagram above |
|
| Communication: | It is your responsibility to
register here for a
(free) FSU computer account so that I can send you email, which you are
expected to check regularly. If you prefer to read your email elsewhere
then you can arrange to have messages
forwarded, but you must still obtain an FSU account in the first
instance |
| Your name: |
 |
|
I don't know who you are, but because
everything works so much better when I do, I would like to
learn your name as soon as possible. So, please take a sheet of
card stock (or even paper), fold it in half, write your name in large letters on
one side and stand it up on your desk so that I can see it.
(Write what you want me to call you: if you're a William who
likes to be called Dubya or a Margaret Jane who likes to be
called Dee Dee, write Dubya or Dee Dee, not William or Margaret
Jane.) Please bring your nameplate to every class
until I have finally learnt your name (which will take
significantly longer than it used to take when I started
out) |
|
| Course format: |
The course will be based on assigned readings consisting of lectures or—occasionally—passages from the text and
on solving problems interactively. After each period I will set
homework for the following period (either in class or by email); for
example, your homework for Monday, January 10 is to read both Lecture 1 and Lecture 2,
and to attempt as many as possible of the associated problems.
In class, I will always assume that you have
both read (not necessarily understood) any assigned readings and at
least attempted (not necessarily completed) a significant and
representative sample of the homework problems. Questions may be asked
at any time (and should be, if there's anything you don't
understand).
On a typical Tuesday or Thursday, I will aim to
end class formally after 50-60 minutes so that I can use the remaining
15-25 minutes of allotted time to offer tutorial help to those who need
it. For other tutorial help, see How to
study |
| Test Format: |
Look at tests from past semesters |
| Calculator policy: |
You are allowed to use a TI-30Xa/TI-36X or a four-function calculator for
tests. The use of any other calculator is strictly
forbidden |
| Grades: |
Will be based on four classroom tests (15% or 20% apiece) and a
cumulative final examination (30%). Note that quality of presentation
is extremely important. It is not enough merely to produce an answer:
you must show all necessary steps in your method, with enough comments
and/or diagrams to convince me that you thoroughly understand.
Precise cut-off points for A, B and C will be
determined by the distribution of grades at the end of the semester,
but are likely be in the vicinity of 90%, 80% and 70%, respectively. In
borderline cases, a smaller number of completely correct solutions will
carry more weight than a proportionate number of fragmentary answers;
later test scores will carry more weight than earlier test scores; and
a record of active participation in class will carry more weight than a
record of passive attendance (in that order of relative importance
among these three factors). Plus or minus grades may be assigned
in a manner consistent with standard University practice.
Please note that partial credit will be awarded
only when part of a solution is completely correct (not when all of a
solution is partially correct, whatever that means, if anything). Also,
a grade of I will not be given to avoid a grade of F or to give
additional study time. Failure to process a course drop will result in
a course grade of F |
| Test solutions: |
Will always be posted online (along with the test itself). There
are two advantages. First, online solutions make grading far more
efficient: instead of writing the same corrections on numerous
manuscripts, I simply identify the point(s) at which a solution goes
awry. Second, the online tests and solutions together form a test bank
for use by students in future years. I caution you, however:
never read my solution to a problem until first of all you have
seriously attempted the problem yourself. If you have at least
made a serious (and I do mean serious) attempt, then—even if you
were unable to complete the problem yourself—you will benefit from
reading my solution to it; if not, then not (rather, you will merely
form a false impression of how well you understand ... as indicated by
the above diagram) |
| Attendance policy: | You are expected to attend class
regularly, and bear the full responsibility for learning anything covered
during any class that you miss |
| Exam policy: |
No makeup exams. An absence may be excused given sufficient
evidence of extenuating circumstances (in which case, extra weight will
be attached to the other exams). But you must either have discussed
the matter with me (well) in advance; or, in the case of illness, have
brought me a note from a physician explicitly stating that you were too
ill to attend class on the day in question; and similarly for other
extenuating circumstances. An unexcused absence will result in a grade of
zero |
| Etiquette: |
You are firmly bound by Florida State University's Academic Honor Code. Briefly, you have the
responsibility to uphold the highest standards of academic integrity in
your own work, to refuse to tolerate violations of academic integrity
in the University community, and to foster a high sense of integrity
and social responsibility on the part of the University community. Even
more briefly, you must neither cheat nor enable others to cheat. The
penalties for violations can be severe. Please carefully read the
section in the FSU Student Handbook on the Honor Code and official
procedures for dealing with students who violate it. If you are in any
doubt at all as to what constitutes acceptable behavior in this regard,
you should ask me for clarification.
You are also bound by the ordinary rules and
customs of polite behavior that prevail in a civilized society. I
assume that you know these rules and customs, and I expect you to
comply with them. (In particular, you are not allowed to use a cell
phone or otherwise have private conversations with others during class.) |
| Probable test dates: |
Tuesday, February 01
Tuesday, March 01
Tuesday, March 29
Tuesday, April 19 |
| Certain final dates: | Section 09: Friday,
April 29, 12:30 — 02:30 p.m. in 106 LOV
Section 10: Friday,
April 29, 03:00 — 05:00 p.m. in 106 LOV |
| How to study: |
There is a lot of material to be covered in this course, so it is
important that you keep up from the very beginning, always attempting
as many as possible (or as necessary) of the homework problems. If you
get stuck, you can go to the Math Help Center: opening hours are posted
here.
Alternatively, you can send me your question by email.
As soon as I possibly can, which might be as soon as within half an
hour, but might also be a day or two later (I have a life, too, you
know), I will reply—not to you, but rather to the class alias
(after carefully concealing your identity, just in case you are
inexplicably bashful about being perceived as smart enough to ask a
question). Often I will attach a PDF file to my reply. If you can't
open it, then I can't help you, because the problem is at your end; and
so you must either fix it (with help from ACNS, if necessary) or
download the file from here instead.
Note, however, the following. First, you must
identify yourself (i.e., you remain anonymous to the other students in
the class, but not to me) in the body of your message (because your username
does not identify you to me): I don't reply to anonymous email. Second,
you must be as specific as possible in describing your difficulty: the
more precisely you identify how you got stuck, the more helpful my
reply is likely to be. |
| Disabilities: | If you have a disability requiring
academic accommodations, then not only should you register with the Student
Disability Resource Center (SDRC),
but also you should bring me written confirmation from SDRC during the
first week of class. This and other class materials are available in
alternative format upon request. |

