Lecture 11: Projective Structures on Surfaces
Let \(\Sigma\) be a closed surface of genus at least 2, and \(\Sigma_2\) a surface of genus \(2\).
Let \(\Gamma=\langle a,b,c,d\rangle\) be a discrete subgroup of \(PSO(2,1)\). Then \(\mathbb{H}^2/\Gamma\cong \Sigma_2\). The surface \(\Sigma\) covers \(\Sigma_2\) and if we let \(\Gamma'\subset \Gamma\) be the subgroup corresponding to this cover then \(\mathbb{H}^2/\Gamma'\) gives a convex projective structure on \(\Sigma\)
Let \(\Omega\subseteq RP^2\) be an open properly convex set, let \(\Gamma\) be a discrete subgroup of \(PGL(\Omega)\), and \(f\colon\Sigma\to \Omega/\Gamma\). Then the pair \((\Omega/\Gamma,f)\) is a marked convex projective structure on \(\Sigma\). There is an equivalence relation on the collection of marked convex projective structures on \(\Sigma\) by saying \((\Omega/\Gamma,f)\sim(\Omega'/\Gamma',f')\) if there is an element \(g\in PGL_3(R)\) so that \(gf\) is isotopic to \(f'\)
Teichmuller space \(T(\Sigma)\) is contained in \(\mathfrak{B}(\Sigma)\), the collection of equivalence classes of marked convex projective structures.
The character variety is \(\chi(\Sigma)=Hom(\pi_1\Sigma,SL_3(R))/SL_3(R)\). There is a map \(Hol\colon B(\Sigma)\to \chi(\Sigma)\), with \(Hol(\Omega/\Gamma,f)=\left[f_*\colon \pi_1\Sigma\to\Gamma\subseteq SL_3(R)\right]\)
Theorem:(Koszul, Goldman-Choi) Hol is a homeomorphism onto a connected component of \(\chi(\Sigma)\).
Theorem:(Goldman) If \(\Sigma\) has genus \(g\geq 2\), then \(\mathfrak{B}(\Sigma)\) is a cell of dimension \(16g-16=-8\chi(\Sigma)\).
Outline:
1 Understand “\(\mathfrak{B}(Pants)\)”. It is an 8-dimensional cell.
2 If \(\Sigma_1\) and \(\Sigma_2\) are convex projective manifolds with “nice” boundary and their boundary geometry agrees, then they can be “convexly glued” in 2-dimensional ways.
###Principal annuli
Let \(D^+=\{\begin{pmatrix} e^{t_1} & & \\ & e^{t_2} & \\ & & e^{t_3}\end{pmatrix}\in SL_3(R)\mid t_3<t_2<t_1\text{ and } t_1+t_2+t_3=0\}\).
Let \(\Delta=\{[e^{x_1},e^{x_2},e^{x_3}\mid x_1+x_2+x_3=0\}\). Let \(1\not=\gamma=\begin{pmatrix} e^{t_1} & & \\ & e^{t_2} & \\ & & e^{t_3}\end{pmatrix}\in D^+\). Then choose \((a_1,a_2,a_3)\) such that \(a_1t_1+a_2t_2+a_3t_3=0\). Then let \(f_\gamma\colon\Delta\to R^+\) with \(f_\gamma([e^{x_1},e^{x_2},e^{x_3}])=e^{a_1x_1+a_2x_2+a_3x_3}\). Then we have \(f_\gamma(\gamma[e^{x_1},e^{x_2},e^{x_3})=f_\gamma([e^{x_1+t_1},e^{x_2+t_2},e^{x_3+t_3}])=f_\gamma([e^{x_1},e^{x_2},e^{x_3}])\).
\(\Delta/\langle\gamma\rangle\) is foliated by the level sets of \(f_\gamma\).
Let \(A_d^\gamma=f^{-1}((d,\infty))/\langle\gamma\rangle\), which we call a principal annulus. Let \(\Sigma=\Omega/\Gamma\) be properly convex with boundary. Let \(\partial\subseteq \partial\Sigma\). We say that \(\Omega/\Gamma\) has principal totally geodesic boundary if for each lift \(\widetilde{\partial}\) of \(\partial\) in \(\widetilde{\Sigma}\), \(D(\widetilde{\partial})\) is an embedding into an open segment in \(RP^1\subseteq RP^2\) and \(\rho(\pi_1\partial)\) conjugate into \(D^+\).
The following picture illustrates the geometry of \(\Omega\) when \(\Omega/\Gamma\) has a principal boundary component and is useful to refer to when thinking about the following two lemmas.
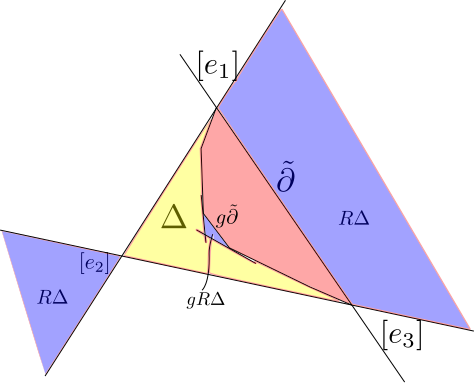
Lemma: If \(\Sigma\cong \Omega/\Gamma\) has principal totally geodesic boundary, then (after applying a projective transformation) \(\Omega\subseteq\overline{\Delta}\) and \(\Sigma\) contains an embedded principal annulus neighborhood of each principal boundary component.
Proof: We can always assume \(\Omega\cap\overline{\Delta}\not=\varnothing\). By construction we know that \([e_1,e_3]\cap\overline{\Delta}\subseteq\partial\Omega\).
Let \(\langle \gamma\rangle=\pi_1\partial\). For a generic \(p\in \Omega^*\), we have \(\gamma^np\to[e_3^*]\in\partial\Omega^*\) as \(n\to\infty\) and \(\gamma^{n}p\to[e_1^*]\in\partial\Omega^*\) as \(n\to -\infty\). As a result we see that \([\ker e_1^\ast]\) and \([\ker e_3^\ast]\) are supporting hyperplanes. As a result we see that \(\Omega\) is disjoint from these hyperplanes and thus \(\Omega\subseteq \overline{\Delta}\).
In order to show that \(\Sigma\) contains an embedded principal annulus we start by taking a regular neighborhood \(N\) of \(\partial\) in \(\Sigma\) and lifting it to \(\tilde N\subset \Omega\). Since \(\partial\) is compact we can find a \(\hat N\subset \tilde N\) which covers a principal annulus in \(\Sigma\). Since \(\hat N\) is contained in \(\tilde N\) and \(N\) is embedded we see that this principal annulus must be embedded.
Let \(R\) be the reflection given in coordinates by \(\begin{pmatrix}1 & & \\ & -1 & \\ & & 1\end{pmatrix}\)
Lemma: If \(g\in \Gamma\setminus\langle\gamma\rangle\), then \(g R\Delta\subseteq \Delta\setminus \Omega\).
Proof: \(\Omega\cap R\Delta=\varnothing\) so \(\varnothing=g(\Omega\cap R\Delta)=\Omega\cap gR\Delta\). Given \(g\in \Gamma\setminus\langle\gamma\rangle\) The set \(gR\Delta\) is bounded by the three lines \(g\tilde \partial\), \(p_1:=g[\ker e_1^\ast]\) and \(p_3=g[\ker e_3^\ast]\). The planes \(p_1\) and \(p_3\) are disjoint from \(R\Delta\) and are thus correspond to points \(p_1^\ast,p_3^\ast\in \partial \Omega^\ast\cap (R\Delta)^\ast\). The projective line \([p_1^\ast,p_3^\ast]\) is disjoint from \(\Delta^\ast\). As a results we see that the pencil of hyperplanes containing \(p_1\) and \(p_3\) has its center in \(\Delta\). Thus \(gR\Delta\subset \Delta\setminus \Omega\).
Next time we will use this setup to show that properly convex surfaces with principal totally geodesic boundary components can be convexly glued together whenever their boundary geometry agrees.
Previous Post: Lecture 10: Properly Convex Automorphisms Part II
Next Post: Lecture 12: Projective Structures on Surfaces Part II