PROBLEMS INVOLVING DISTANCE AND THE PYTHAGOREAN THEOREM
The Pythagorean Theorem
The Pythagorean Theorem states the relationship between the lengths of the three sides of a right triangle:

C2 = A2 + B2, where A and B are the lengths of the two shorter sides (the legs) and C is the length of the longer side (the hypotenuse).
EXAMPLE 2.5.1
Find the missing side length for each triangle shown below.

There are two figures. The first figure shows a right triangle where one leg measures 5 inches and the other leg measures 8 inches. The hypotenuse is labeled x.
The second figure shows a right triangle where one leg measures 16 centimeters, the second leg is labeled x, and the hypotenuse measures 20 centimeters.
see solutions
EXAMPLE 2.5.2
The diagram below shows the rectangular pen in which Gomer confines his wolverines and badgers. In order to prevent the wolverines from dating the badgers, Gomer is going to build a fence running from one corner of the pen to the opposite corner, thus dividing the pen into two smaller pens. Assuming that construction of such a fence will cost $1.25 per foot, find the total cost of this fence.

The figure shows a rectangle whose length is 40 yards and whose width is 20 yards. A diagonal (the fence)
runs from the lower left corner to the upper right corner, dividing the rectangle into two right triangles, one of which
is labeled "wolverines" while the other is labeled "badgers."
A. $4500
B. $500
C. $168
D. $56
see solution
EXAMPLE 2.5.3
The figure below shows the Math Department's plan to run a computer cable (w) from the top of the Algebra Building (A) to the top of the Trig Tower (T). Find the total cost of the cable, assuming that it costs $3.50 per foot. (The front faces of the buildings, and the cable, are all in the same plane.)
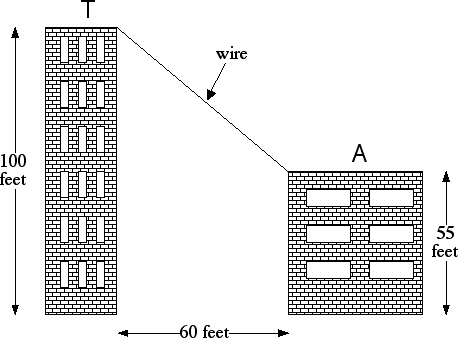
The figure shows two buildings, labeled A and T respectively. Building T is 100 feet tall. Building A is 55 feet tall and is located to the right of building T. The distance between the two buildings is 60 feet. The wire, labeled w, runs from the top right corner of T to the toop left corner of A.
A. $75
B. $21
C. $263
D. $753
see solution
EXAMPLE 2.5.4
The diagram below shows the path the Plato takes when he goes for a philosophical stroll.
Plato starts at home, proceeds to the toga shop, then heads north to the tunic store, then returns home. On average, Plato thinks one profound thought for every 10 yards that he walks. Find the total number of profound thoughts that he will think during this walk.

The figure shows a right triangle. The Toga Store is located at the right angle, while Home and the Tunic Shoppe are located at the other two corners, respectively. The distance from Home to the Tunic Shoppe is 260 yards (this is the hypotenuse of the right triangle). The distance from Home to the Toga Store is 240 yards (this is one leg of the right triangle). The distance from the Toga Store to the Tunic Shoppe is not given (this is the other leg of the right triangle).
A. 60
B. 10
C. 100
D. 258
E. None of these
see solution
EXAMPLE 2.5.5
The diagram below shows Gomer's sailboat at anchor. At the time that he released the anchor, the sailboat was touching the channel marker buoy shown in the figure. After he has drifted 80 feet from the bouy he has let out 160 feet of anchor line. How deep is the water under the bouy?
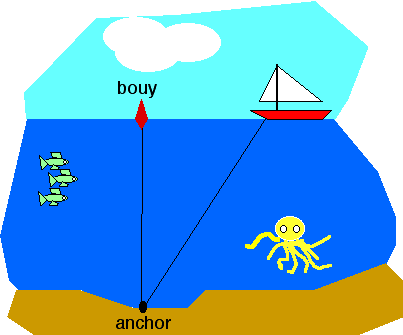
The figure shows a right triangle. One leg of the right triangle is the distance from the bouy to the anchor. The second leg is the distance from the bouy to the boat (80 feet). The hypotenuse is the distance from the anchor to the boat (160 feet).
A. 60 feet
B. 179 feet
C. 80 feet
D. 139 feet
see solution
EXAMPLE 2.5.6
Find the distance around the racetrack shown below.

The racetrack consists of a rectangle with half a circle atttached to the left side and half a circle attached to the right side. The length of the rectangle is 300 feet. The width of the rectangle, which coincides with the diameter of each half circle, is 200 feet.
A. 0.23 miles
B. 0.48 miles
C. 0.0067 miles
D. 0.35 miles
see solution
The previous problem required use of the following fact from elementary geometry:
The CIRCUMFERENCE of a circle
The distance around a circle is called its circumference, and is determined by the circle's radius or diameter:

The figure shows a circle. The diameter of the circle is labeled D, and the radius is labeled r. The circumference is C. The figure shows two formulas:
1. C = two times pi times r
2. C = pi times D
EXAMPLE 2.5.7
How fast (in miles per hour) does the Earth travel as it orbits the sun? (Note: the Earth's orbit is approximately circular, with a radius of 93,000,000 miles.)
EXAMPLE 2.5.8
The diagram on the left below shows the race course for the 40-K Wolverine Day Fun Run. The diagram on the right shows the course modified by the short-cut that Gomer uses. What distance does Gomer cover if he runs the race using his short-cut?

There are two figures. The first figure, labeled "Actual race course," shows a square where each side measures 10 kilometers. The second figure, labeled "Gomer's short cut," shows the same square truncated so that it has become a five sided figure. This is the figure that results when a right triangle with legs measuring 8 kilometers and 6 kilometers, respectively, is removed from the upper right corner of the original square.
A. 36 km
B. 26 km
C. 10 km
D. 16 km
EXAMPLE 2.5.9
Plato and Aristotle are loitering on the street corner, when suddenly Socrates (to whom they owe money) shows up. Plato takes off running eastward at a rate of 16 miles per hour, and Aristotle runs southward at a rate of 12 miles per hour. How far apart (direct distance) are Plato and Aristotle after 15 minutes?

The figure shows a right triangle. Socrates stands at the right angle, waving his arms. To his east, Plato is shown running eastward. The leg of the triangle between Socrates and Plato is labeled "16 miles per hour." Directly south of Socrates, Aristotle is shown running southward. The leg of the triangle connecting Socrates and Plato is labeled "12 miles per hour." The hypotenuse of the triangle is the distance between Aristotle and Plato.
see solution
Download practice exercises (PDF file)