Solution to EXAMPLE 2.1.8 #2
Step 1: Determine the number of rows required.
Since the statement
contains two basic variables (the fact that there are multiple occurrences of q is not significant), the truth table will require four rows (22 = 4). Step 2: Determine the number of columns required.
There will be one column for each basic variable, and one column for each occurrence of a logical connective in the statement
. This means that we will have a total of six columns (one column for p, one for q, and one for each of the four connectives). Step 3: Begin filling in the columns.
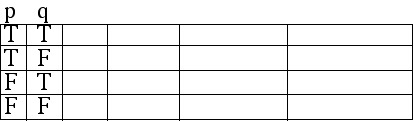
The first two columns represent the basic variables p, q.
We label them accordingly, and fill them in in such a way that each row takes into account a different combination of truth values for these basic variables. The configuration shown below is standard.
Step 4: Label the remaining columns, bearing in mind which simpler components are
required in order to construct the statement 
.
In order to construct the statement 
, we need a column for q and a column for 
; we already have a column for q, but in order to make this column for 
we first need a column for 
; however, in order to make this column for 
we need a column for ~p. We will label these columns before filling them in.
The column for ~p will be the opposite of the column for p:
To fill in the column for 
we compare the column for ~p with the column for q, bearing in mind the behavior of the "and" connective: the only time 
will be TRUE is when ~p and q are both true; in any row where ~p is false, or q is false, or both, the statement 
will be false:
The fill in the column for 
, we refer to the column for 
; the column for 
will be the opposite of the column for 
:
Finally, we fill in the column for 
. To do this, we refer to the column for q along with the column for 
, bearing in mind the behavior of the "or" connective; The statement 
will be TRUE if q is true, or if 
is true, or both; it will be false only in the case where q and 
are both false.
