EXAMPLE 2.1.1
Solution to EXAMPLE 2.1.8 #1

Step 1: Determine the number of rows required.

Since the statement contains two basic variables, the truth table will require four rows, because 2² = 4.



Step 2: Determine the number of columns required.

There will be one column for each basic variable, and one column for each occurrence of a logical connective in the statement . This means that we will have a total of four columns.













 

Step 3: Begin filling in the columns.

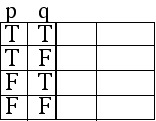
The first two columns represent the basic variables p, q.

We label them accordingly, and fill them in in such a way that each row takes into account a different combination of truth values for these basic variables. The configuration shown below is standard.

 

STEP 4: Label the remaining columns, bearing in mind which simpler components are required in order to construct the statement .

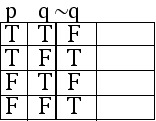
In order to construct the statement , we need a column for p and a column for ~q. The truth table already has a column for p, so we now label the next column ~q. We fill in this column be referring to the values in the column for q; every entry in the column ~q will be the opposite of the corresponding entry in the column for q:

 

Now that we have a column for p as well as a column for ~q, we can combine them to construct a column for . We fill in this column by referring to the columns for p and for ~q, and bearing in mind the behavior of the "or" connective: will be TRUE in any row where the column for p is true, or the column for ~q is true, or both; will be FALSE only in a row where the p and ~q are both false.

 

 

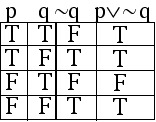
This complete truth table shows the behavior of the statement in every conceivable situation. As we will see later, it can be used to compare the statement with other compound statements, and to identify other, different-looking statements that are equivalent to .