Drawing Perfect (Correct)
Parabolas

I have seen many miserable, horrible attempts to draw an approximation to a parabola in other instructors' handouts, tests, and quizzes. The freely available drawing utilities like MS Paint, and the drawing utility within MS Word, cannot create an accurate parabola.

Bézier Curves

Within the LaTeX picture environment, there is quadratic bézier curve drawing primitive. TeXdraw also has a bézier curve available, but it uses a cubic curve. To draw a parabola, a quadratic curve is precisely what we need.

The command for the bézier curve in LaTeX is

\qbezier(x1, y1)(x2, y2)(x3, y3)

The curve begins at the point (x1, y1) and ends at the point (x3, y3). The point (x2, y2) is the control point. The curve is drawn so that it is tangent to the line through (x1, y1) and (x2, y2) at (x1, y1), and tangent to the line through (x2, y2) and (x3, y3) at (x3, y3).

An Example

As an example, let's create the graph of f (x) = x2 − 6x + 7.
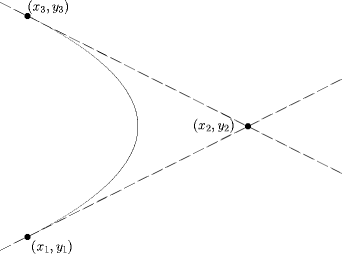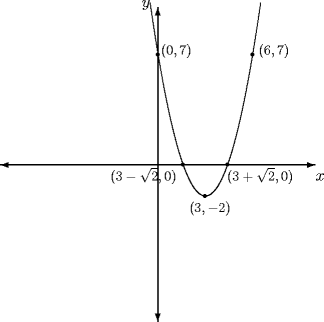
Planning
We begin by finding the axis of symmetry. The control point will lie on the axis of symmetry.


We can also find the location of the vertex:


Now, choose two points for the start and end of the parabola. I am choosing points 4 units to the left and right of the axis of symmetry, (-1, 14) and (7, 14). Of course, this will vary for each graph you want to create.

Using a little calculus, find the equation of the tangent line at the point (-1, 14).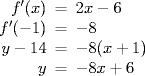

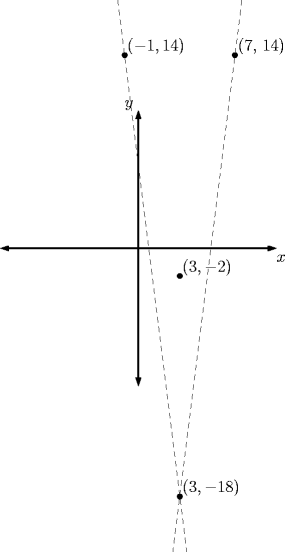
The control point is y(3) = −18.
Graph It
Now all that remains is to sketch the parabola with the \qbezier command. We would also like to identify some points on the graph, such as x- and y-intercepts. Using the same coordinate system as I did with Cartesian graph paper, the coordinates are appropriately scaled and shifted. The relevant code fragment and the resulting picture are shown below. 

\setlength{\unitlength}{.8 mm}
\begin{picture}(100,100)

%Draw the x- and y-axes and label them
\thicklines
\put(50,50){\vector(0,1){50}}
\put(50,50){\vector(1,0){50}}
\put(50,50){\vector(0,-1){50}}
\put(50,50){\vector(-1,0){50}}
\put(100,45){$x$}
\put(45,100){$y$}

%Draw the parabola and label some points
\qbezier(45,120)(65,-40)(85,120)

% y-intercept
\put(50,85){\circle*{1.5}}
\put(51,85){\footnotesize $(0,7)$}

% Another point using symmetry
\put(80,85){\circle*{1.5}}
\put(82,85){\footnotesize $(6,7)$}

% x-intercepts
\put(72.071,50){\circle*{1.5}}
\put(72,45){\footnotesize $(3+\sqrt{2},0)$}

\put(57.9289, 50){\circle*{1.5}}
\put(35,45){\footnotesize $(3-\sqrt{2},0)$}

$ Vertex
\put(65,40){\circle*{1.5}}
\put(60,35){\footnotesize $(3,-2)$}

\end{picture}
Clean It Up
Having completed the sketch, I see a couple of refinements that will result in a more pleasing graph.

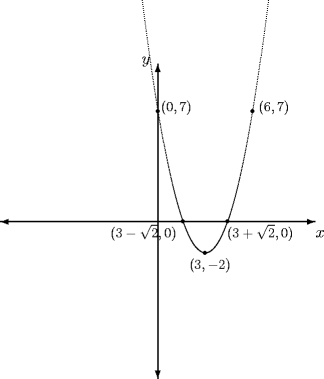
First, the graph doesn't need to be so tall. Instead of starting at (−1, 14) and ending at (7, 14), perhaps we could start at (−0.5, 10.25) and end at (6.5, 10.25). Repeating the work from above, we find that the control point is now (3, −14.25).
Second, notice how the parabola "tapers" at the ends? The \qbezier command takes an optional argument "num" 
\qbezier[num](x1, y1)(x2, y2)(x3, y3)
num is the number of samples taken to draw the curve—it is actually drawn as a series of dots, equally sampled between x1 and x3. When y has a relatively low rate of change with respect to x, as it does in the neighborhood of the vertex, we get a smooth curve. When y varies relatively rapidly, we begin to see the individual dots that make up the curve. How do we fix it? We partly take care of the problem by using a shorter curve. We can also increase the sampling rate. In the code above, we change the line for the bézier curve to 
\qbezier[1000](47.5,101.25)(65,-21.25)(82.5,101.25)
to produce the graph at the right.
num = 1000
For comparison, here are the results for the default value of num, and for num equal to 100.

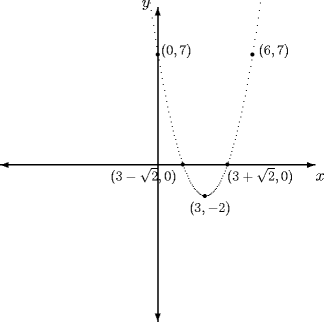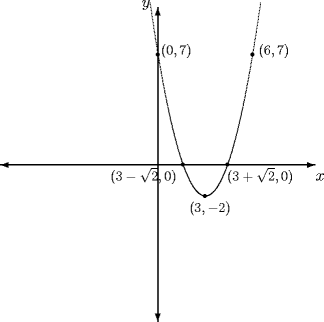num = 100 num = default value