| > | #Lab 5 |
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | L:=15:tail:={y1(t),y2(t)},numeric,initstep=0.1,range=0..L; |
![]()
| > | alpha:=0.5; SYS:=diff(y1(t),t)=-y1(t)*(y1(t)^2-alpha)-y2(t),diff(y2(t),t)=y1(t); A1a:=dsolve([SYS, y1(0)=2,y2(0)=2],tail): A1b:=dsolve([SYS, y1(0)=-2,y2(0)=2],tail): A1c:=dsolve([SYS, y1(0)=0.3,y2(0)=0],tail): P1a:=odeplot(A1a,[y1(t),y2(t)],t=0..L,color=red,numpoints=1000): P1b:=odeplot(A1b,[y1(t),y2(t)],t=0..L,color=blue,numpoints=1000): P1c:=odeplot(A1c,[y1(t),y2(t)],t=0..L,color=black,numpoints=1000): display(P1a,P1b,P1c,title=cat("alpha = ",convert(alpha,string))); |
![]()
![]()
![[Maple Plot]](images/lab54.gif)
| > | alpha:=1.0; SYS:=diff(y1(t),t)=-y1(t)*(y1(t)^2-alpha)-y2(t),diff(y2(t),t)=y1(t); A2a:=dsolve([SYS, y1(0)=2,y2(0)=2],tail): A2b:=dsolve([SYS, y1(0)=-2,y2(0)=2],tail): A2c:=dsolve([SYS, y1(0)=0.3,y2(0)=0],tail): P1a:=odeplot(A2a,[y1(t),y2(t)],t=0..L,color=red,numpoints=1000): P1b:=odeplot(A2b,[y1(t),y2(t)],t=0..L,color=blue,numpoints=1000): P1c:=odeplot(A2c,[y1(t),y2(t)],t=0..L,color=black,numpoints=1000): display(P1a,P1b,P1c,title=cat("alpha = ",convert(alpha,string))); |
![]()
![]()
![[Maple Plot]](images/lab57.gif)
| > | alpha:=1.5; SYS:=diff(y1(t),t)=-y1(t)*(y1(t)^2-alpha)-y2(t),diff(y2(t),t)=y1(t); A3a:=dsolve([SYS, y1(0)=2,y2(0)=2],tail): A3b:=dsolve([SYS, y1(0)=-2,y2(0)=2],tail): A3c:=dsolve([SYS, y1(0)=0.3,y2(0)=0],tail): P1a:=odeplot(A3a,[y1(t),y2(t)],t=0..L,color=red,numpoints=1000): P1b:=odeplot(A3b,[y1(t),y2(t)],t=0..L,color=blue,numpoints=1000): P1c:=odeplot(A3c,[y1(t),y2(t)],t=0..L,color=black,numpoints=1000): display(P1a,P1b,P1c,title=cat("alpha = ",convert(alpha,string))); |
![]()
![]()
![[Maple Plot]](images/lab510.gif)
| > | alpha:=2.0; SYS:=diff(y1(t),t)=-y1(t)*(y1(t)^2-alpha)-y2(t),diff(y2(t),t)=y1(t); A4a:=dsolve([SYS, y1(0)=2,y2(0)=2],tail): A4b:=dsolve([SYS, y1(0)=-2,y2(0)=2],tail): A4c:=dsolve([SYS, y1(0)=0.3,y2(0)=0],tail): P1a:=odeplot(A4a,[y1(t),y2(t)],t=0..L,color=red,numpoints=1000): P1b:=odeplot(A4b,[y1(t),y2(t)],t=0..L,color=blue,numpoints=1000): P1c:=odeplot(A4c,[y1(t),y2(t)],t=0..L,color=black,numpoints=1000): display(P1a,P1b,P1c,title=cat("alpha = ",convert(alpha,string))); |
![]()
![]()
![[Maple Plot]](images/lab513.gif)
| > | alpha:=2.5; SYS:=diff(y1(t),t)=-y1(t)*(y1(t)^2-alpha)-y2(t),diff(y2(t),t)=y1(t); A5a:=dsolve([SYS, y1(0)=2,y2(0)=2],tail): A5b:=dsolve([SYS, y1(0)=-2,y2(0)=2],tail): A5c:=dsolve([SYS, y1(0)=0.3,y2(0)=0],tail): P1a:=odeplot(A5a,[y1(t),y2(t)],t=0..L,color=red,numpoints=1000): P1b:=odeplot(A5b,[y1(t),y2(t)],t=0..L,color=blue,numpoints=1000): P1c:=odeplot(A5c,[y1(t),y2(t)],t=0..L,color=black,numpoints=1000): display(P1a,P1b,P1c,title=cat("alpha = ",convert(alpha,string))); |
![]()
![]()
![[Maple Plot]](images/lab516.gif)
| > | display(odeplot(A1b,[y1(t),y2(t)],t=L/3..L,color=red,numpoints=1000), odeplot(A2b,[y1(t),y2(t)],t=L/3..L,color=blue,numpoints=1000), odeplot(A3b,[y1(t),y2(t)],t=L/3..L,color=green,numpoints=1000), odeplot(A4b,[y1(t),y2(t)],t=L/3..L,color=brown,numpoints=1000), odeplot(A5b,[y1(t),y2(t)],t=L/3..L,color=red,numpoints=1000), title="limit cycles for alpha = 0.5, 1.0, 1.5, 2.0 and 2.5"); |
![[Maple Plot]](images/lab517.gif)
| > | ODE:=diff(y(t),t,t)-9*y(t)=0; |
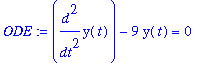
| > | IC:=y(0)=1,D(y)(0)=-3; |
![]()
| > | dsolve({ODE,IC},y(t)); |
![]()
| > | P2:=dsolve({ODE,IC},numeric,y(t),initstep=0.1); |
![]()
| > | L:=14:display(plot(exp(-3*t),t=0..L,color=blue),odeplot(P2,t=0..L)); |
![[Maple Plot]](images/lab522.gif)
| > | P2(14); |
![]()
| > | for i from 0 to 50 by 1 do P2(i); od; |
| > | SYS:=diff(y1(t),t)=y2(t),diff(y2(t),t)=9*y1(t),y1(0)=1,y2(0)=-3; |
![]()
| > | Run:=dsolve([SYS],numeric,range=0..13); |
![]()
| > | display(fieldplot([y,9*x],x=-1..1,y=-3..3,arrows=thick),odeplot(Run,[y1(t),y2(t)],t=0..12.5,thickness=3)); |
![[Maple Plot]](images/lab526.gif)
| > | for i from 5 to 13 do Run(i); od; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | SYS2:=diff(y1(t),t)=y2(t),diff(y2(t),t)=y1(t),y1(0)=1,y2(0)=-1; |
![]()
| > | Run2:=dsolve([SYS],numeric); |
![]()
| > | Run2(126.0); |
![]()
| > |